SESION 5-M3-P4-22

 

 

“Año del Fortalecimiento de la soberanía nacional” 

MATERIAL DE LECTURA-S5-P4-3°G-22

 

PRIMERA PARTE:

1.1.- DENOMINACION DE LA SESION 5:

“Determinamos líneas y puntos de un triángulo”

1.2.- PROPOSITO DE LA SESION 5:

Al finalizar la SESIÓN 4, el estudiante del TERCER GRADO de secundaria, RESOLVERA problemas, modelando líneas y puntos notables de un TRIANGULO.

1.3.- SITUACION SIGNIFICATIVA.

Un alumno muy Emprendedor, de la I.E “San Carlos” del distrito de Monsefú, se ha propuesto diseñar el local de su futura empresa; por lo que, pretende utilizar TRIANGULOS y para eso se pregunta: ¿Qué elementos debo conocer? ¿Cómo podría identificarlos?

   Como alumnos, del Tercer Grado: ¿Podrías ayudarle?, ¿De qué manera?

 

SEGUNDA PARTE: LECTURAS.

2.1.- LINEAS Y PUNTO NOTABLES EN UN TRIANGULO:

2.1.1.- DEFINICIÓN:

En un triángulo se pueden trazar cuatro tipos de líneas notables: ALTURAS, MEDIANAS, MEDIATRICES y BISECTRICES.

2.1.2.- ALTURA Y ORTOCENTRO:

La altura de un triángulo, es el segmento perpendicular que va desde un vértice hasta la recta que contiene al lado opuesto a este. En un triángulo se pueden construir TRES alturas, una por cada vértice. Para construir las alturas de un triángulo, se utilizan ESCUADRAS y las rectas que contienen las alturas, se intersecan en un mismo punto llamado ORTOCENTRO.

 

2.1.3.- MEDIANA Y BARICENTRO:

La mediana de un triángulo, es un segmento cuyos extremos son el vértice y el punto medio del lado opuesto, dando origen a TRES medianas, una por cada vértice, ubicando primero los puntos medios de cada lado y luego, se trazan los segmentos que unen cada vértice, con el punto medio del lado opuesto, y se intersecan en un mismo punto llamado BARICENTRO.

En cualquier tipo de triángulo, el BARICENTRO cumple las siguientes propiedades:

• Siempre está en el interior del triángulo.

• La longitud entre el baricentro y cada uno de los vértices equivale a 2/3 de la longitud de la mediana que contiene a dicho vértice.

 

 

2.1.4.- BISECTRIZ E INCENTRO:

La bisectriz de un ángulo, es una semirrecta que lo divide en dos ángulos congruentes. En el caso del ángulo interno de un triángulo, la bisectriz, puede considerarse como un segmento cuyos extremos son el vértice y un punto del lado opuesto, y que divide el ángulo en dos congruentes. Para construir una bisectriz de un triángulo con regla y compás, se procede así:

Las bisectrices de un triángulo se intersecan en un punto llamado INCENTRO. El incentro equidista de los lados del triángulo.

2.1.5.- MEDIATRIZ Y CIRCUNCENTRO:

La mediatriz de un segmento, es una recta perpendicular que pasa por su punto medio y en un triángulo se pueden trazar tres mediatrices; una por cada lado.

Las mediatrices también se pueden construir con regla y compás. Para ellos, se realizan los siguientes pasos:

Las mediatrices de un triángulo se intersecan en un mismo punto llamado CIRCUNCENTRO y equidista de los vértices del triángulo.

2.1.6.- RESUMEN:

En un triángulo, no necesariamente las líneas notables deben coincidir, por ejemplo en el triángulo cuyos lados tienen longitudes diferentes, las líneas notables no coinciden.

 

 

 

2.1.6.- PROPIEDADES DE ANGULOS DETERMINADOS POR BISECTRICES.

1.- De un ángulo interior y un ángulo exterior: “La medida de un ángulo formado por una bisectriz interior y una bisectriz exterior, que parten de dos vértices diferentes, es igual a la mitad de la medida del tercer ángulo del triángulo”.

 

 

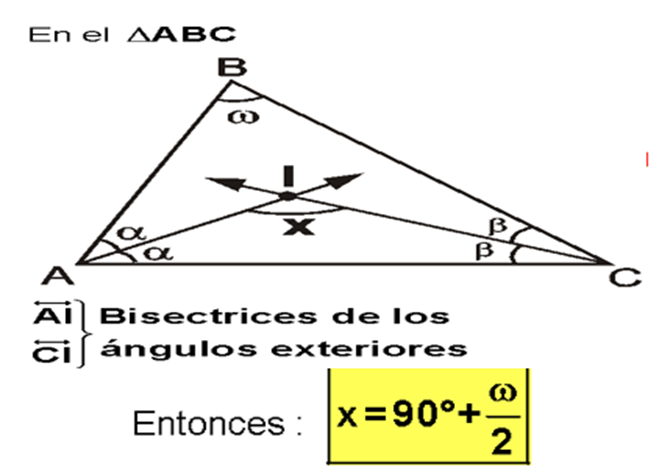
2.- Angulo determinado por las bisectrices de dos ángulos interiores: “La medida del ángulo que forman dos bisectrices interiores de un triángulo es igual a 90° más la mitad del tercer ángulo del triángulo”.

 

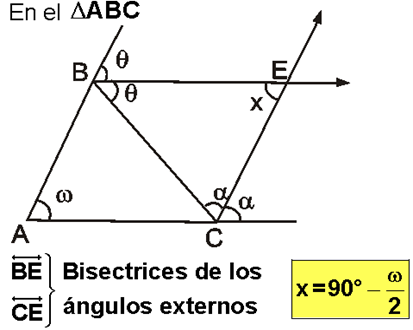
3.- Angulo determinado por las bisectrices de dos ángulos exteriores: “La medida del ángulo formado por dos bisectrices exteriores es igual a 90° menos la mitad del tercer ángulo del triángulo”.

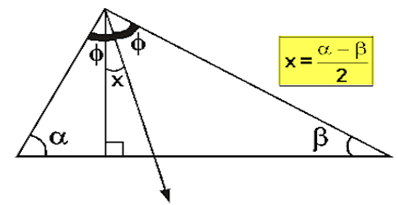
4.- Angulo formado por una altura y la bisectriz interior trazada desde el mismo vértice: “La medida es igual a la semidiferencia de las medidas de los otros dos ángulos del triángulo”.

 

 

TERCERA PARTE:

VIDEOS DE REFURZO: Ingresar a los siguientes links y analizar:

3.1.- LINEAS Y PUNTOS NOTABLES DE UN TRIANGULO.

https://www.youtube.com/watch?v=q4C65NXyKUg

CUARTA PARTE: Teniendo en cuenta lo leído y visualizado, resuelve lo siguiente:

PROBLEMAS:

1.- La altura relativa a la base de un triángulo isósceles mide 21. Calcular la distancia del baricentro a dicha base.

a) 6                              b) 2                            c)21                             d) 14                               e) 7 

2.- Calcular “x” en la figura:

a) 20°                              b) 40°                         c)  60°                          d) 70°                        e) 55°     

 3.- Calcular “Ɵ” en la figura:

a) 55°                              b) 45°                         c)    35°                          d) 65°                        e) 60°  4.- 4.- Calcular “X” en la figura, si “I” es INCENTRO.

a) 20°                              b) 30°                         c)    40°                          d) 50°                        e) 60°

5.- Calcular “X” si “O” es ortocentro del ΔABC. Además, “I es INCENTRO del ΔAOC:

a) 120°                              b) 130°                         c)   140°                          d) 150°                        e) 160°

6.- En un triángulo “ABC” se traza la ceviana “BE” tal que: AB = BE = CE    y  BCE = 38°.

Hallar “m ݻ A”

a) 64°                              b) 76°                         c)   72°                          d) 68°                        e)  80°

7.- De la figura, calcular “X”: Si AE es bisectriz interior.

 

a) 20°                              b) 30°                         c)  40°                          d) 70°                        e)  35°

 

8.- En un triángulo, se traza la bisectriz interior BE, calcular :

a) 45°                              b) 30°                         c)  62°                          d) 65°                        e)  75°

9.- Dado el triángulo “PQR”, se traza la bisectriz interior PM, tal que: PQ = PM = MR. Calcular:

a) 20°                              b) 30°                         c)  37°                          d) 53°                        e)  36°

10.- En la figura BH es la altura, además:

a) 20°                              b) 30°                         c)  60°                          d) 40°                        e)  80°

 

QUINTA PARTE: Actividades de reflexión.

Después de haber realizado tu trabajo, reflexiona con tus compañeros respondiendo las siguientes preguntas:

¿Para qué nos son útiles determinar las líneas y puntos notables de un TRIANGULO?, ¿Podrías comentar en qué otras situaciones podemos utilizar dichos conocimientos?, ¿Cómo has identificado dichos ELELEMENTOS en la resolución de problemas?,¿Qué elementos relevantes has reconocido en ellas? , ¿Qué dificultades encontraste y que hiciste para superarlas?, ¿por qué crees que algunos tienen una respuesta diferente?, ¿qué nociones relacionaste?, ¿cuáles fueron las que más encontraste?

 

SEXTA PARTE:

6.1.- PRODUCTO: RESOLVER la situación significativa, en una hoja previamente entregada por el docente, tomando como referencia los conocimientos aprendidos y compartidos en el aula de acuerdo a la sesión desarrollada.

6.2.- ENTREGA: En físico, de manera presencial.

¡ BUENA SUERTE ¡

Vallejos MARRUFO, Elías.

PROFESOR

“No digas ¡cuando tenga tiempo estudiaré!, porque quizás nunca tendrás tiempo” (Hilel, Pirkei Avot).