CARP.RECU-2022-MATEMATICA

 

“Año del Bicentenario del Perú: 200 años de independencia” 

CARPETA DE RECUPÉRACION - 2022

AREA: MATEMATICA 3°GRADO DE SECUNDARIA

 

I.- PRESENTACION

La presente Carpeta de Recuperación, tiene como finalidad que los y las estudiantes logren las competencias propuestas en el área de Matemática, que por diversos motivos no se lograron en el año 2021. Cada Experiencia de aprendizaje y sus actividades, está relacionada con el Proyecto Institucional denominado: "Desde la matemática desarrollamos EMPRENDIMIENTO en familia y comunidad, para fortalecer la economía en nuestro hogar, con actividades auténticas"; es decir que, en cada actividad planteada, tenemos en cuenta la puesta en marcha de su negocio emprendedor por parte del alumno y su familia durante el estado de la pandemia en nuestra región. Con responsabilidad y entusiasmo puedes desarrollar esta Carpeta en tu cuaderno o folder y lo presentarás en marzo, cuando retornes a tus clases.

  

II.- ORIENTACIONES GENERALES:

Reciban nuestro cordial saludos, alumnos de la I.E “San Carlos” del distrito de Monsefú, especialmente los alumnos del 3°Grado de secundaria. La presente carpeta de Recuperación, tiene cuatro experiencias de aprendizaje con sus respectivas actividades que debes desarrollar después de leer con atención las fuentes y observar las imágenes. Recuerda registrar tus respuestas en el cuaderno u hojas de tu portafolio o grabar un audio; porque, después volverás a utilizar esta información. Al finalizar cada experiencia de aprendizaje, desarrollaras un PRODUCTO que lo deberás presentar al finalizar el programa.

DURACION: Periodo vacacional

PERIODO DE EJECUCION: 08 semanas

CICLO Y GRADO:  VII - 3° Grado

 

III.- EXPERIENCIAS DE APRENDIZAJE.

 

3.1.- EXPERIENCIA DE APRENDIZAJE N°01: “Conocemos las Medidas de Dispersión”

SITUACION SIGNIFICATIVA Nos encontramos en un contexto de oportunidad que nos permite reflexionar con nuestras familias sobre la importancia de ejecutar un plan de negocio. Todo ello a pesar de la incertidumbre producto de la PANDEMIA que aún estamos viviendo y las diversas problemáticas y tensiones que afectan la convivencia en la diversidad. MARYORI estudiante de la institución educativa “San Carlos” de Monsefú, pretende sustentar su economía, a base de alternativas que se le ha presentado, como: "Producción y venta de yogurt, vinagre, vino y encurtidos". Ello le ha ocasionado una gran incertidumbre en su elección. ¿Cómo podemos ayudarle? o ¿Qué podemos sugerirle?

RETO: Ante esta situación, nos planteamos: ¿Debería dedicarse a la producción y venta de todos los productos? ¿Es más rentable? o sólo ¿Dedicarse a uno solo?

PROPOSITO: “EXPRESAR con diversas representaciones y lenguaje matemático, su comprensión de la DISPERSION en relación con la media para datos no agrupados”.

PRODUCTO: PRODUCTO: CUADRO DOBLE ENTRADA Para la elaboración de esta tabla de doble entrada, se tendrá en cuenta la base teórica de las fuentes.

COMPETENCIA: “Resuelve Problemas de Gestión de Datos e Incertidumbre”

 

 

ACTIVIDAD N°01: Aplicamos la desviación estándar y sus elementos.

Leeremos las fuentes sobre la DESVIACION ESTANDAR, para poderla aplicar en el desarrollo de un problema concreto, según el negocio emprendedor aplicado. Te proponemos que hagas una lectura a profundidad, de cada una de las fuentes para seguir compendiando y reflexionando sobre la desviación estándar, su utilidad y aplicación a la solución de problemas reales

  

FUENTE N°01: Las MEDIDAS DE DISPERSION, son parámetros que miden la separación de los datos de una distribución respecto a su media. Entregan información, sobre la variación de la variable. Pretenden resumir en un solo valor, la dispersión que tiene un conjunto de datos. Las medidas de dispersión más utilizadas son: Rango de variación, Varianza, Desviación estándar, Coeficiente de variación, Desviación media. a) RANGO = v. máx. – v. min. b) VARIANZA: Depende si es de población o muestra. Ojo: Para hallar “mu = µ”

 

 

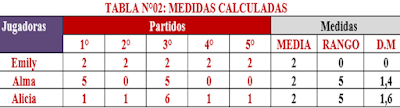
FUENTE N°02: El director técnico de la I.E San Carlos de Monsefú, debes de seleccionar a una jugadora para la posición de delantera, del equipo femenino de futbol; pero, hay tres jugadoras para el puesto: Emily, Alma                       y Alicia. Según el cuadro: 1.- ¿Cuál sería la seleccionada, si el criterio es la que mete más goles? 2.- ¿Cuál sería la seleccionada, si usamos el rango y la deviación media? SOLUCION Para la primera pregunta: Al analizar la tabla y hacer uso de la aritmética, las tres jugadoras han anotado 10 goles en total en los cinco partidos. RESPUESTA: N.A Para la segunda pregunta: Usar sólo la aritmética, no permite tomar una decisión, por eso, en este caso se utiliza parte de la estadística para seleccionar una jugadora. 1°) TOMAR UN SEGUNDO CRITERIO: Calcula la MEDIA ARITMÉTICA de los goles de las jugadoras, es decir, calcula el promedio de goles de cada una. Esto implica sumar los goles y dividirlos entre 5 que es el número total de partidos jugados. (FORMULA “mu = µ”) PARA EMILY:      (2+2+2+2+2)/5  = 10/5 = 2 PARA ALMA:        (5+0+0+5+0)/5 = 10/5 = 2 PARA ALICIA: (1+1+6+1+1)/5 = 10/5 = 2 El promedio de las tres es el mismo y con esta información aún no se podría tomar una decisión. 2°) TOMAR UN TERCER CRITERIO: Calculamos el RANGO: Rango = V. máx. – V. mín. EMILY: Valor máximo - valor mínimo = 2 – 2 =  0. ALMA: Valor máximo - valor mínimo = 5 – 0 = 5. ALICIA: Valor máximo - valor mínimo = 6 – 1 = 5. Por el momento, una de las jugadoras se podría descartar, por tener un RANGO BAJO; pero, aún hay dos jugadoras con el mismo rango. Con la información del rango, todavía no puedes tomar una decisión. 3° TOMAR UN CUARTO CRITERIO: Ahora calcula la DESVIACIÓN MEDIA para cada una de las jugadoras y se espera que con esta medida de dispersión, sea posible tomar la decisión. (FORMULA Dx) Los valores obtenidos de la DESVIACIÓN MEDIA de cada jugadora indican qué, tan lejos están del promedio, lo cual es el punto de comparación. ALICIA es la jugadora que más se aleja del promedio, con 1,6; en cuanto a ALMA, es 1,4 y EMILY es “0”; por lo tanto, es la UNICA que está dentro del promedio. Con estos datos, ahora sí se puede tomar la decisión como director(a) técnico(a), ¿a quién escogerías de las tres? RESPUESTA: “Lo anterior permite elegir a EMILY, quien tienen el mejor desempeño en los partidos, no sólo por anotar goles, sino por mantener un ritmo constante de anotaciones en los cinco partidos.

 

DESARROLLAMOS LA ACTIVIDAD DE LA EXPERINCIA DE APARENDIZAJE N°01

 

1.- Luego de la lectura de las fuentes, aplica a la solución del presente caso real: “Un alumno del TERCER GRADO de Secundaria se ha dedicado a la venta de los siguientes productos: “yogurt, vinagre, vino y encurtidos”, durante un mes, según la tabla adjunta:

PRODUCTOS	VENTA SEMANAL
	1°S	2°S	3°S	4S
YOGURT	2	4	6	2
VINAGRE	0	1	8	5
VINO	3	4	3	4
ENCURTIDOS	8	0	6	0

 a) Completa la siguiente tabla: 

PRODUCTOS	VENTA SEMANAL				MEDIDAS
	1°S	2°S	3°S	4S	RANGO	MEDIA	D.M
YOGURT	2	4	6	2
VINAGRE	0	1	8	5
VINO	3	4	3	4
ENCURTIDOS	8	0	6	0

 

b) Contesta según los datos consignados en la tabla de doble entrada:

1°)  ¿Qué producto sería el seleccionado, si el criterio es el que más se ha vendido?

2°) ¿Qué producto sería el seleccionado, si usamos el rango y la deviación media?

3°) ¿Cuáles serían los dos productos que podría vender con seguridad?

 

2.- NOS AUTOEVALUAMOS:

CRITERIOS DEEVALAUCION	Lo logr	Estoy en proceso de lograrlo	¿Qué puedo hacer para mejorar mis aprendizajes?
COMPRENDI que la Desviación Estándar, es parte de la estadística.
UTILICÉ las medidas de dispersión: Rango de variación, Varianza, Desviación estándar, Coeficiente de variación, Desviación media, para la solución de problemas reales.
EXPRESE con diversas representaciones y lenguaje matemático, la comprensión de la DISPERSION en relación con la media para datos no agrupados.
PROPUSE problemas reales aplicando la Desviación Estándar, para hallar su solución.

  

3.2.- EXPERIENCIA DE APRENDIZAJE N°02: “Expresamos notaciones exponenciales y científicas”

SITUACION SIGNIFICATIVA MARYORI estudiante del TERCER Grado de secundaria de la institución educativa “San Carlos” de Monsefú, ha decidido dedicarse a la Producción y venta de “yogurt, vinagre, vino y encurtidos". Pero, tiene dificultad en proyectarse en la elaboración y venta de cantidades inmensas; sobre todo, al expresarlas numéricamente. Esto la lleva a pensar, en la cantidad de ceros que pudiera tener un número ¿Cómo podemos ayudarla? ¿Qué nociones debe adquirir?

RETO: A partir de la situación, nos preguntamos: Si en Monsefú existieran aproximadamente 10 billones de hogares y cada una tiene alrededor de 400 000 millones de Soles, ¿cuántos soles en total se reunirían aproximadamente en la ciudad de Monsefú? ¿Escribe los valores numéricos en notación científica?

PROPOSITO: “EXPRESAR con diversas representaciones y lenguaje numérico su comprensión de la utilidad de expresar cantidades muy grandes en NOTACIÓN EXPONENCIAL y NOTACIÓN CIENTÍFICA, en la aplicación de un problema referente a su plan de negocio”.

PRODUCTO: PRODUCTO: CUADRO DOBLE ENTRADA Para la elaboración de esta tabla de doble entrada, se tendrá en cuenta la base teórica de las fuentes y ejemplos.

COMPETENCIA: “Resuelve Problemas de Cantidad”

  

ACTIVIDAD N°02: La NOTACION y sus tipos.

Leeremos las fuentes sobre la NOTACIÓN EXPONENCIAL y NOTACIÓN CIENTÍFICA, para poderla aplicar en el desarrollo de un problema concreto, según el negocio emprendedor aplicado.

Te proponemos que hagas una lectura a profundidad, de cada una de las fuentes para seguir compendiando y reflexionando sobre dichas NOTACIONES, su utilidad y aplicación a la solución de problemas reales.

 

FUENTE 1 1.- NOTACIÓN MATEMÁTICA: La matemática se apoya en un lenguaje simbólico formal, que sigue una serie de convenciones propias. Los símbolos representan un concepto, una relación, una operación, o una fórmula matemática según ciertas reglas. Estos símbolos no deben considerarse abreviaturas, sino entidades con valor propio y autónomo. 2.- NOTACIÓN EXPONENCIAL: Consiste en escribir un número a partir de un producto entre otros 2 números, uno llamado coeficiente y el otro llamado potencia de base 10, cuyo exponente es un número entero. El coeficiente debe cumplir una con condición, de que sea mayor o igual a 10:  coeficiente ≥ 10 Ejemplos: 500 = 50 . 101    ;   500 000 000 000 000 = 50 . 1013   ;   0,00000004 = 40. 10-9 3.- NOTACIÓN CIENTIFICA: Es una forma de escribir los números que acomoda valores demasiado grandes o pequeños ​para ser escrito de manera convencional. El uso de esta notación, se basa en potencias de 10. El exponente o mantista es elegido de manera que el valor absoluto de “m” permanezca al menos uno pero menos de diez: 1 ≤ | m | <10. Ejemplo: 100 000 000 000 = 1 . 1011 0, 000 000 000 01 = 1 . 10-11 4.- OPERACIONES CON N. CIENTIFICA Y N. EXPOENCIAL 4.1.- SUMA Y RESTA EN NOTACIÓN CIENTÍFICA: Sus elementos deben tener el mismo exponente en la potencia de 10. Una vez tenemos esto, resolvemos. 4.2.- MULTIPLICAR Y DIVIDIR EN NOTACIÓN CIENTÍFICA; Para realizar las operaciones hay que tener en cuenta las propiedades de las potencias; luego, se multiplican los números que están delante de la potencia de 10 y por otro, se multiplican las potencias de 10, manteniendo la base y sumando los exponentes y si es división se restan sus exponentes.

 

FUENTE 2 EJEMPLOS: Realizar las siguientes operaciones: a.- 1,25 . 102 – 0,37 . 103 + 6,14 . 103   SOLUCION   1,25 . 102 – 0,37 . 103 + 6,14 . 103  = 1,25 . 102 – 3,70 . 102 + 61,40 . 102   = 58,95 . 102   = 5,895 . 103  Respuestas: La celeste es en NOTACION EXPONENCIAL y la roja es en NOTACION CIENTIFICA.   b.- 0,486 . 10-5 + 93 . 10-9 – 6  . 10-7  SOLUCION    0,486 . 10-5 + 93 . 10-9 – 6  . 10-7    = 48,6 . 10-7      +  0,93 . 10-7   –  6  . 10-7  0,486 . 10-5 + 93 . 10-9 – 6  . 10-7    = (48,6   +   0,93   –  6)  . 10-7  0,486 . 10-5 + 93 . 10-9 – 6  . 10-7    = (49,53   –  6)  . 10-7  0,486 . 10-5 + 93 . 10-9 – 6  . 10-7    = 43,53  . 10-7  0,486 . 10-5 + 93 . 10-9 – 6  . 10-7    = 4,353  . 10-6  Respuestas: La celeste es en NOTACION EXPONENCIAL y la roja es en NOTACION CIENTIFICA. c.- 5,78 . 103 . 2,47 . 105 SOLUCION 5,78 . 103 . 2,47. 105 = (5,78 . 2,47) (105 . 103) 5,78 . 103 . 2,47. 105 = (14,2766) (105+3) 5,78 . 103 . 2,47. 105 = 14,2766 . 108 5,78 . 103 . 2,47. 105 = 1,42766 . 109 Respuestas: La celeste es en NOTACION EXPONENCIAL y la roja es en NOTACION CIENTIFICA.   d.- (3,18 . 104 .  1,26 . 10-2) SOLUCION   3,18 . 104 .  1,26 . 10-2 = (3,18 .  1,26) (104 .  10-2) 3,18 . 104 .  1,26 . 10-2  = (4,0068) (104-2) 3,18 . 104 .  1,26 . 10-2  = 4,0068 . 102   e.- (6,87 . 105) / (5,21 . 108) = SOLUCION 8,79 .102 : 2,31 . 10-5  =  (8,79 : 2,31) (102 : 10-5) 8,79 .102 : 2,31 . 10-5  =  (3,8052) (102-(-5)) 8,79 .102 : 2,31 . 10-5  =  3,8052 . 107

 

DESARROLLAMOS LA ACTIVIDAD DE LA EXPERIENCIA DE APARENDIZAJE N°02

 

1.- Luego de la lectura de las fuentes, aplica a la solución del presente caso real: “Una tienda, con 40 mil trabajadores, está dedicada a la venta de: yogurt, vinagre, vino y encurtidos. Pretende en un año, lo siguiente: En yogurt, producir 40 millones, en vinagre, producir 50 millones, en vino, producir 10 millones, y en encurtidos, producir 2 millones. Si son 9 sucursales que pretenden producir la misma cantidad; además, si 18 millones de productos, se repartirá al personal. Si la diferencia, se pretende embarcar en 3 camiones”.

a) Completar la siguiente tabla:

  

PRODUCTO	VALOR REAL	NOTACION CIENTFICA
YOGURT
VINAGRE
VINO
ENCURTIDOS

 

b) Contesta:

1°) ¿Cuál es la cantidad a vender, en notación científica en una sola tienda?

2°) ¿Cuál es la cantidad a vender, en notación científica en las 3 tiendas?

3°) ¿Cuántos productos llevaría cada camión?

2.- Luego de la lectura del RETO de la experiencia de aprendizaje 2 contesta:

¿Cuántos soles en total se reunirían aproximadamente en la ciudad de Monsefú? ¿Escribe los valores numéricos en notación científica?

 

3.- NOS AUTOEVALUAMOS:

CRITERIOS DEEVALAUCION	Lo logre	Estoy en proceso de lograrlo	¿Qué puedo hacer para mejorar mis aprendizajes?
COMPRENDI la diferencia que existe entre la Notación EXPONENCIAL y la Notación CIENTIFICA.
UTILICÉ la Notación EXPONENCIAL y la Notación CIENTIFICA, en la solución de problemas reales.
EXPRESE con diversas representaciones y lenguaje la comprensión de la utilidad de expresar cantidades muy grandes en Notación EXPONENCIAL y Notación CIENTIFICA.
PROPUSE problemas reales aplicando la Notación EXPONENCIAL y la Notación CIENTIFICA.

 

 

3.3.- EXPERIENCIA DE APRENDIZAJE N°03: “Diferenciamos los crecimientos aritméticos y geométricos”

SITUACION SIGNIFICATIVA MARYORI estudiante del TERCER Grado de secundaria de la institución educativa “San Carlos” de Monsefú, ha puesto en marcha su negocio emprendedor sobre: “Producción y venta de yogurt, vinagre, vino y encurtidos”,  y al haber cumplido un año del negocio, necesita saber qué tipo de crecimiento MATEMATICO, ha existido en su negocio. ¿Cómo podemos ayudarla? ¿Qué nociones debe adquirir? MARYORI estudiante de la institución educativa “San Carlos” de Monsefú,¿Cómo podemos ayudarla? ¿Qué tipo de orientación necesita?

RETO: A partir de la situación, nos preguntamos: ¿Cómo se plantearía un problema de venta de productos para hallar la diferencia de CRECIMIENTOS?

PROPOSITO: “PLANTEAR afirmaciones sobre las diferencias entre CRECIMIENTO ARITMÉTICO y GEOMÉTRICO, que descubre en la solución de problemas de su negocio emprendedor”.

PRODUCTO: CUADRO DOBLE ENTRADA Para la elaboración de esta tabla de doble entrada, se tendrá en cuenta la base teórica de las fuentes y ejemplos.

COMPETENCIA: “Resuelve Problemas de Regularidad, Equivalencia y Cambios”

 

 

ACTIVIDAD N°03: El CRECIMIENTO matemático y sus tipos.

Leeremos las fuentes sobre la CRECIMIENTO ARITMÉTICO y GEOMÉTRICO, para poderla aplicar en el desarrollo de un problema concreto, según el negocio emprendedor aplicado. Te proponemos que hagas una lectura a profundidad, de cada una de las fuentes para seguir compendiando y reflexionando sobre dichos CRECIMIENTO, su utilidad y aplicación a la solución de problemas reales.

 

FUENTE 1 1.- CRECIMIENTO ARITMETICO: Son los fenómenos que se describen con funciones del tipo (a + rt) y la sucesión de números de la forma:  a, a +r, a+ 2r, a +3r, a +4r, a +5r…. es una Sucesión de crecimiento aritmético. 2.- CRECIMIENTO GEOMETRICO: También conocido como exponencial, es aquella progresión que aumenta por multiplicación de una cantidad constante. Su FORMULA es: A (1 + r) n =  3.- GRAFICA DEL CRECIMIENTO ARITMETICO:  4.- GRAFICA DEL CRECIMIENTO GEOMETRICO:

 

FUENTE 2 EJEMPLOS:  1.- Juan tiene un negocio emprendedor, dedicado a la venta de productos artesanales, al revisar sus ventas ha detectado que: En 2019 ha vendido 176 495 productos y en 2020 vendió unos 187 185. Si el crecimiento anual es Constante ¿Cuántos productos habrá vendido en el año 2022? SOLUCION 1° Hallamos el crecimiento anual: año 2020 – año 2019 = 187 185 - 176 495 = 10 690 que es la “”r” 2° Para el año 2022 habrá: N° inicial de ventas + (Tiempo) (Incremento constante) = (a + rt) Reemplazando: año 2019 + 10 690 (4) = 176 495   + 42 760 = 219 255 Productos   2.- Una familia emprendedora, deposita en el banco S/100 000. Si la tasa de interés es 25% anual y los intereses reinvierten como capital cada año ¿cuál es el capital depositado después de tres años? SOLUCION 1° Sacando datos: A = 100 00 ; r = 25%  = 0,25  ; t = 3 años 2° Reemplazando en la FORMULA: A (1 + r) n 100 000 (1 + 0,25) 3 =  100 000 (1,25) 3 =  100 000 (1,95)  = 195 000 3° Respuesta: El capital depositado después de 3 años es S/195 000

 

DESARROLLAMOS LA ACTIVIDAD DE LA EXPERIENCIA DE APARENDIZAJE N°03

 

1.- Luego de la lectura de las fuentes, aplica a la solución del presente caso real: “Elsa dedicada a la “Producción y venta de yogurt, vinagre, vino y encurtidos”, en un primer momento decide abrir una cuenta bancaria con 3 mil soles, con una tasa de interés simple de 30% al año. En un segundo momento, decide que los intereses reinviertan como capital cada año.

 A) Completa la siguiente tabla:

 

CRECIMIENTO	AÑOS
	1°	2°	3°	4°	5°	6°
Aritmético (1° momento)
Geométrico (2° momento)

 

B) Contestar:

1°) ¿Cuánto dinero tendrá en 6 años?

2°) Si los intereses reinvierten como capital cada año ¿cuál es el capital depositado después de 6 años?

 

2.- NOS AUTOEVALUAMOS:

CRITERIOS DEEVALAUCION	Lo logre	Estoy en proceso de lograrlo	¿Qué puedo hacer para mejorar mis aprendizajes?
COMPRENDI las diferencias que existe entre Crecimiento ARITMETICO y Crecimiento GEOMETRICO.
UTILICÉ las definiciones de Crecimiento ARITMETICO y Crecimiento GEOMETRICO, para la solución de problemas reales.
PLANTEE afirmaciones sobre las diferencias entre Crecimiento ARITMETICO y Crecimiento GEOMETRICO, descubiertas en la solución de problemas de mi negocio emprendedor.
PROPUSE problemas reales aplicando nociones de Crecimiento ARITMETICO y Crecimiento GEOMETRICO.

 

 

3.4.- EXPERIENCIA DE APRENDIZAJE N°04: “Identificamos las relaciones y propiedades de las figuras geométricas”

SITUACION SIGNIFICATIVA MARYORI estudiante del TERCER Grado de secundaria de la institución educativa “San Carlos” de Monsefú, ha elaborado diseños de envases para usarlos en su negocio de: “Producción y venta de yogurt, vinagre, vino y encurtidos"; pero, tiene dificultad en la combinación de modelos, formas y tamaños ¿Cómo podemos ayudarla? ¿Qué nociones debe adquirir?

RETO: A partir de la situación, nos preguntamos: ¿Se podría ELABORAR y COMPLETAR un cuadro de doble entrada, sobre las RELACIONES y PROPIEDADES de las figuras geométricas usadas para los envases de tu PLAN de negocio?”

PROPOSITO: “PLANTEAR afirmaciones sobre las RELACIONES Y PROPIEDADES que descubre entre OBJETOS, entre OBJETOS y FORMAS geométricas y entre FORMAS geométricas”.

PRODUCTO: PRODUCTO: CUADRO DOBLE ENTRADA Para la elaboración de esta tabla de doble entrada, se tendrá en cuenta la base teórica de las fuentes.

COMPETENCIA: “Resuelve Problemas de Forma, Movimiento y Localización”

 

 

ACTIVIDAD N°04: Las Figuras Geométricas.

Leeremos las fuentes sobre las FIGURAS GEOMETRICAS, para poderla aplicar en el desarrollo de un problema concreto, según el negocio emprendedor aplicado. Te proponemos que hagas una lectura a profundidad, de cada una de las fuentes para seguir compendiando y reflexionando sobre dichas FIGURAS, su utilidad y aplicación a la solución de problemas reales.

 

FUENTE 1 1.- LAS FIGURAS GEOMÉTRICAS. Conocer las figuras geométricas básicas, como son: cuadrados, rectángulos, círculos y triángulos, supone el poder establecer RELACIONES con su entorno más cercano e inmediato. 2.- RELACIONES GEOMÉTRICAS ENTRE FIGURAS. Para entablar una RELACION, debemos tener de 2 a más figuras; pues, 2 figuras pueden tener entre sí, una serie de relaciones geométricas atendiendo a su FORMA, TAMAÑO o DISPOSICIÓN. Además, dichas RELACIONES pueden ser, tanto gráficas como métricas y puede haber dentro de estos dos grupos otras a su vez (igualdad, equivalencia, semejanza). 2.1.- IGUALES: Dos figuras son iguales, cuando sus FORMAS y TAMAÑOS son los mismos. Si se superponen dos figuras iguales, sus puntos coinciden; por lo tanto, mantienen la misma área. 2.2.- SEMEJANTES: Dos figuras son semejantes, cuando tienen IDÉNTICA forma y tamaño DIFERENTE. En el caso de las formas poligonales, los ángulos son iguales y los lados proporcionales; por lo tanto, distinta área. 2.3.- EQUIVALENCIA: Dos figuras son equivalentes, cuando tienen distinta forma pero mantienen el mismo área. 2.4.- SIMÉTRICAS: Dos figuras son simétricas, cuando tienen idéntica forma y tamaño, pero una DISPOSICIÓN diferente. Es una relación de igualdad entre dos figuras, en la que cada punto se corresponde con otro de modo que ambos equidistan de un eje (AXIAL), de un centro (CENTRAL) o de un plano de simetría (BILATERAL). 3.- PROPIEDADES DEL TRIANGULO: 3.1.- PROPIEDADES FUNDAMENTALES: N° PROPIEDAD FUNDAMENTAL FORMULA 1° SUMA DE SUS ANGULOS INTERNOS α + β + ϴ = 180° SUMA DE SUS ANGULOS EXTERNOS ɸ + Ѡ + ϒ = 360° 2° SUMA DE 2 ANGULOS INTERNOS CON UN EXTERNO OPUESTO α + β = Ѡ 3° RESPECTO A SUS LADOS: Si  a   <  b   <  c  c - b  <  a   <  b + c c - a  <  b  <  a + c b - a  <  c  <  a + b   3.2.- PROPIEDADES PARTICULARES:   N° PROPIEDAD PARTICULAR FORMULA 1 LA MARIPPOSA α + β =  ϴ + ϒ 2 TRES ANGULOS INTERNOS RESPECTO A UN EXTERNO EN LA BASE α + β +  ϴ  =  ϒ 3 DOS ANGULOS INTERNOS OPUESTOS DE UN ROMBO RESPECTO A DOS EXTERNOS OPUESTOS α + β  =  ϴ  +  ϒ 4 DOS ANGULOS DE CUADRILATERO RESPECTO A 2 ANGULOS EXTERNOS OPUESTOS α + β  =  ϴ  +  ϒ

 

 

FUENTE 2 EJEMPLOS: Aplicar las propiedades y resolver. 1.- Hallar el valor de “x” y del ángulo alfa de la figura adjunta:   SOLUCION   1°) Halando “α”: 5 α +24° + 2 α + α + 30° = 180° 8 α  = 180° - 54°  α  = 126° : 8 α  = 15,75° 2°) Halando “x”: Aplicamos: c – b  <  a <  b + c    c – b  <  a <  b + c    5 – 2  <  x <  5 + 2    3  <  x <  7    Luego: x = {4, 5, 6} Por lo tanto, los valores de “x” puede ser:     V.Max. = 6   y el     V.Min. = 4

 

DESARROLLAMOS LA ACTIVIDAD DE LA EXPERIENCIA DE APARENDIZAJE N°02

 

1.- Luego de la lectura de las fuentes, aplica a la solución del presente caso real: “Se pretende diseñar un envase de forma triangular, ya se tiene la primera parte y tiene la forma de una “mariposa” formado por 2 triángulos opuestos (uno frente al otro), cuyos ángulos de la base del ΔABC (izquierda) miden 50° y 2x y los ángulos de la base del ΔA’B’C’ (derecha) miden 4x y 30°”.

a) Contestar:

1°) ¿Cuál es el valor de “x”?

2°) ¿Cuál es el valor de “2x”?

3°) ¿Cuál es el valor de “4x”?

 

b) Completar la siguiente tabla:

 

FIGURAS	VALOR DE CADA ANGULO			VALOR TOTAL DE ANGULOS DEL TRIANGULO
	A/A’	B/B’	C/C’
ΔABC
ΔA’B’C’

 

2.- NOS AUTOEVALUAMOS:

CRITERIOS DEEVALAUCION	Lo logre	Estoy en proceso de lograrlo	¿Qué puedo hacer para mejorar mis aprendizajes?
COMPRENDI las RELACIONES y PROPIEDADES de las figuras geométricas.
UTILICÉ las RELACIONES y PROPIEDADES de las figuras geométricas, para la solución de problemas reales.
PLANTE afirmaciones sobre las RELACIONES y PROPIEDADES que descubrí entre OBJETOS, entre OBJETOS y FORMAS geométricas y entre FORMAS geométricas.
PROPUSE problemas reales aplicando las RELACIONES y PROPIEDADES de las figuras geométricas.

 

 

 

 

 

......................................................

Vallejos MARRUFO, Elías.

PROFESOR

 

 

 

 

 

 

“Educar es más que dar carrera para vivir, es templar el alma para las dificultades y para soportar las injusticias” –PITÁGORAS