SESION 7-M3-P3-22

 

“Año del Fortalecimiento de la soberanía nacional”

MATERIAL DE LECTURA S7-M3-P3-2022

PRIMERA PARTE

1.1.- DENOMINACIÓN DE LA SESIÓN 7:

“Unificamos centros de acumulación y quemado de basura, en nuestro país y distrito”

1.2.- PROPOSITO DE LA SESION 7:

Al finalizar la sesión, el estudiante ENTIENDE la importancia de la intersección de dos funciones y cómo encontrar dicha intersección.

1.3.- SITUACION SIGNIFICATIVA:

“Los vecinos de un sector del distrito de Monsefú, ante la acumulación de basura en distintos puntos del distrito, deciden junto a la municipalidad asignar un punto estratégico para que las personas acudan a esos lugares y así reducir la acumulación de basura. Donde los volquetes de la municipalidad, a cierta hora llegan para recoger la basura.

Ante esta medida, Marcos un vecino que ayuda a combatir esta problemática. Se pregunta: ¿cuál será el recorrido que deberá realizar? ¿Y en qué tiempo podrá interceptar a dichos volquetes de basura?, ¿Qué variables se requieren para calcular las interrogantes Marcos?, ¿Y Cómo calcular dicha intersección?

Como estudiantes de la I.E San Carlos, identificados con la problemática de nuestro distrito: ¿Podemos brindarle nuestra ayuda?, ¿De qué manera?

SEGUNDA PARTE: LECTURAS

2.1.- ¿Qué es una función?

Una función, en matemáticas, es el término usado para indicar la relación o correspondencia entre dos o más cantidades.

Dos variables  y  están asociadas de tal forma que al asignar un valor a “x” entonces, por alguna regla o correspondencia, se asigna automáticamente un valor a “y”, se dice que y es una función (unívoca) de “x”. La variable “x”, a la que se asignan libremente valores, se llama variable independiente, mientras que la variable “Y”, cuyos valores dependen de la “x”, se llama variables dependientes.

2.2.- ¿En dónde podemos en contar una función?

Las funciones dentro de la vida cotidiana no pasan desapercibidas y se utilizan en la Economía, Administración, Física, Biología, Medicina, Investigación, para conocer el crecimiento de una población, la propagación de una epidemia, en la vida real y en otras ciencias etc.

Dando ejemplos de cómo la función lineal puede estar representada en todo aquello que se manejan variables donde el uno depende del otro, donde la propagación de una bacteria se puede expandir aún más con el paso de las horas, como en la investigación cuantitativa es necesario utilizar variables las cuales ayudan en desarrollo de una investigación, por ejemplo:

Variable independiente: Las estrategias didácticas.

Variable dependiente: Modelo pedagógico, el plan de estudios, logros.

2.3.- ¿QUÉ ES UN FUNCIÓN LÍNEAL Y CÓMO SE REPRESENTA?

Una función lineal es un tipo de función polinómica de primer grado, es decir, que puede escribirse bajo la expresión algebraica:

(donde m y b son valores constantes), y cuya representación gráfica en el plano cartesiano es una línea recta.

Las constantes de una función lineal son elementos importantes a la hora de la representación gráfica, ya que la pendiente m indica el grado de inclinación de la recta y la ordenada al origen b indica el punto en que la recta corta al eje y.

2.4.- TIPOS DE FUNCIONES LINEALES.

2.5.- COMO SABER QUE ESTAMOS FRENTE UNA FUNCIÓN LÍNEA.

- Una función es lineal si es de primer grado y su gráfica es una línea recta. En ella no hay productos de variables sólo figuran elevadas a la primera potencia, y no hay variables en ningún denominador, es decir:

- No puede haber una multiplicación de dos o más variables.

- La variable debe de estar elevada a la primera potencia quiere decir que su grado sea uno.

- No puede haber una división donde la variable esté en el denominador.

EJEMPLO: ¿Cuál de las siguientes funciones son lineales?

2.6.- REPRESENTACIONES DE UNA FUNCIÓN LINEAL.

2.7.- PUNTOS DE INTERSECCIÓN CON EL EJE “X”, EJE “Y”.

Si queremos de una función encontrar la o las interseccion(es) con el eje “y”, debo volver la variable “x” igual a 0 y así encontraré el punto de corte, despejando.

Para encontrar la o las intersecciones en el eje “x”, debemos volver la variable “y” igual a 0, es decir, igual la ecuación a 0 y despejar.

Veamos algunos ejemplos:

EJEMPLO 1: Encontrar los puntos de intersección del eje de las ordenadas y abscisas de la: 

f(x) = -2x +4 

SOLUCION:

INTERSECCIÓN CON EJE “Y”:

X = 0

Reemplazando: f(x) = -2x + 4

Y = -2(0) + 4  = 0 + 4 = 4

P (0 , 4)

INTERSECCIÓN CON EJE “X”:

Y = 0

Reemplazando: f(x) = -2x + 4

 0 = -2x + 4

x =  4 : 2

x =  2

P (2 , 0)

GRAFICA Y TABULACIÓN:

2.8.- PUNTOS DE INTERSECCIÓN DE DOS FUNCIONES LINEALES.

Suponga que f(x) y g(x) son dos funciones que toman una entrada de número real, y una salida de número real.

Entonces los puntos de intersección de f(x) y g(x) son aquellos números “x” para los cuales 

f(x) = g(x) 

Algunas veces los valores exactos pueden encontrarse fácilmente al resolver la ecuación 

f(x) = g(x)  algebraicamente.

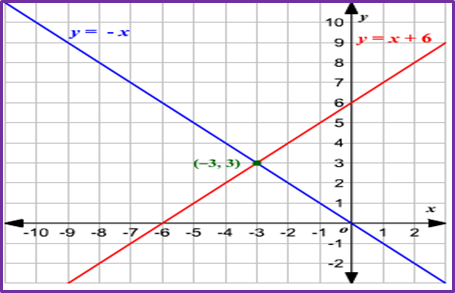
EJEMPLO: Si  f(x) = x + 6  ,  g(x) = - x ¿Cuáles son los puntos de intersección de las funciones f(x) y g(x)?

SOLUCIÓN:

Primero Igualamos: f(x) = g(x)

x +6  = -x

x + x  = -6

2x   = -6

x   = -6 : 2

x   = -3

Segundo reemplazamos en cualquiera de las funciones nos tendrá que salir el mismo resultado:

Por lo tanto, punto intersección es (-3,3)

GRÁFICA

2.9.- PUNTO DE EQUILIBRIO DEL MERCADO.

Si el precio de cierto artículo es demasiado alto, los consumidores no lo adquieren, mientras que si es demasiado bajo los proveedores no lo venden. Si existe un precio para el cual la cantidad demandada por los consumidores es igual a la cantidad ofrecida por los productores, a ese precio se lo llama de equilibrio del mercado.

La función de oferta es la ecuación que representa la cantidad fabricada de un bien en función de su precio y/o otras variables relevantes.

La función de demanda es una ecuación que explica cómo se determina la cantidad demandada de un bien.

TERCERA PARTE

3.1.- VIDEOS DE REFUERZOS: Ingresar a los siguientes links y analizar:

3.1.1.- Funciones LINEALES - Tipos.

https://www.youtube.com/watch?v=sx_gTbPhBIg

3.1.2.- Intersección entre funciones lineales

https://www.youtube.com/watch?v=mbqMHquLW0Q

3.2.3.- Graficar funciones lineales usando las intersecciones.

https://www.youtube.com/watch?v=L8EuB1jRIJE

 

CUARTA PARTE: Teniendo en cuenta lo leído y visualizado, resuelve lo solicitado en cada actividad.

Actividad 1: A partir de la lectura, contestar:

¿Qué es función?

¿En dónde podemos apreciar una función en la vida continuada? Ejemplifica

¿Qué es una función Lineal? ¿Cuáles son sus características?

¿Cómo podemos encontrar el punto de intersección? ¿Qué estrategia utilizarías?

¿Qué significa que dos funciones se intercepten en punto?

¿Cómo podemos encontrar la intersección con el eje de las ordenas y las abscisas? ¿Qué estrategias utilizarías?

¿Qué significa el punto de equilibrio? Explicar con tus propias palabras.

Actividad 2: Encontrar el punto de intersección en las funciones. Representa la gráfica en el plano cartesiano.

P (-3,2)            b) P (2,-2)      c) P (3,2)      d) P (5,2)      e) N.A

 

 P (2,-1)           b) P (3,2)        c) P (-2,1)         d) P (3,2)     e) NA

 

P (1,3)           b) (3,4)           c) P (3,-5)          d) P (2,-4)    e) N.A

Actividad 3: PROBLEMAS

P1: Si se sabe que los vecinos de la junta vecinal de Monsefú, desean obtener contenedores de basura para combatir la acumulación de basura. Pero antes de la adquisición se enteran que la oferta está en función de 0(x) = 50 + Px  donde  Px = precio y también se sabe que la demanda está en función de D(x) = 200 – 4Px  

 ¿Cuál será el precio cuándo el mercado se encuentre en equilibrio?

s/ 10          b) s/12          c) s/ 15          d) s/20       e) N.A

¿Cuántos contenedores pueden adquirir cuando el precio está en equilibrio?

140           b) 130           c) 160            d) 110         e) N.A

P2: Cielo y Kiara se recorren distintos sectores de Monsefú con la el objetivo de poder repartir afiches que concienticen a las personas de no quemar ni acumular basura. Si se sabe que Cielo realiza su recorrido en función de: R(x) = 10x , Kiara en función de: R(x) = 35 + 5x; donde “x” son minutos. Además, se sabe que en cierto punto de encuentran ambas amigas.

a) ¿En qué tiempo se encuentran Cielo y kiara?

b) ¿Cuál habrá sido el recorrido de cada una, cuando se encontraron?

QUINTA PARTE.

Después de haber realizado tu trabajo, reflexiona con tus compañeros respondiendo las siguientes preguntas.

¿Para qué es útil saber sobre una función? ¿Para qué lo aprendiste? ¿Pueden explicar con sus propias palabras que significa cuándo se intersecan don funciones lineales? ¿Qué dificultades encontraste y que hiciste para superarlas? ¿por qué crees que algunos tienen una respuesta diferente?, ¿qué nociones relacionaste?, ¿cuáles fueron las que más encontraste? ¿Qué es el punto de equilibrio? ¿Para que nos sirve lo aprendido en nuestra vida cotidiana?

SEXTA PARTE.

 RETO: Completar los cuestionarios propuestos resolviendo las preguntas, dada por el docente en aula de acuerdo a la sesión desarrollada.

 ENTREGA: En físico, de manera presencial.

¡BUENA SUERTE ¡

SESION 7-MAT.3-P2-22

 

 “Año del Fortalecimiento de la soberanía nacional” 

MATERIAL DE LECTURA-S7-P2-3°G-22

 

PRIMERA PARTE:

1.1.- DENOMINACION DE LA SESION 7:

“Exploramos formas geométricas extraídas de un contexto, para su diseño en los paños matrimoniales”  

1.2.- PROPOSITO DE LA SESION 7:

Al finalizar la sesión, el estudiante PLANTEARA afirmaciones sobre las relaciones y propiedades básicas de las figuras geométricas, en relación a los objetos de su realidad.

1.3.- SITUACION SIGNIFICATIVA.

“MARIANA, estudiante del 3°Grado de secundaria de la I.E “San Carlos de Monsefú”, pretende graficar figuras geométricas de su entorno en la confección de paños y fajas matrimoniales; por lo que, necesita tener un conocimiento amplio sobre sus elementos para sus diseños: ¿Qué figuras geométricas debería conocer? ¿Cuáles son sus elementos básicos a considerar?

 

SEGUNDA PARTE: LECTURAS.

2.1.- ELEMENTOS GEOMÉTRICOS FUNDAMENTALES: Punto, línea y plano son los elementos geométricos básicos con los que podemos dibujar todas las figuras geométricas.

Se denominan propios, si pertenecen a un espacio finito e impropios si están en el infinito.

Los límites de un cuerpo son las superficies, de las superficies las líneas y de las líneas los puntos.

2.1.1.- Punto: Queda definido por la intersección de dos líneas, se designa con letra mayúscula.

2.1.2.- Línea recta: es una sucesión de puntos alineados sin principio ni final. Se designa con letra minúscula.

1°- TIPOS DE RECTAS:

-Rectas secantes: dos rectas serán secantes si se cortan en un punto.

-Rectas paralelas: las rectas serán paralelas si no se cortan en ningún punto.

-Rectas coincidentes: dos rectas serán coincidentes si todos sus puntos son comunes.

-Rectas perpendiculares: dos rectas serán perpendiculares si al cortarse forman cuatro ángulos iguales, es decir, de 90o.

2°- SUBTIPOS DE RECTAS:

a.- Semirrecta: Cuando la recta tiene un origen concreto en un espacio finito (propio) y el otro extremo está en el infinito (impropio).

b.- Segmento: cuando está limitada por ambos extremos por puntos.

c.- Línea curva: Es una sucesión de puntos que no están alineados o en la misma dirección.

 

2.1.3.- Plano: Tienen dos dimensiones, una sola dimensión las líneas y ninguna dimensión los puntos, que únicamente determinan un lugar.

Está formado por infinitas rectas y no tiene límites. Se designa con letra mayúscula –a menudo del alfabeto griego–.

 

2.2.- ELEMENTOS GEOMÉTRICOS ESPECIFICOS:

2.1) ÁNGULOS:

Ø    DEFINICIÓN.- Es la parte del plano, comprendida entre dos semirrectas de origen común.

Los lados del ángulo son las dos semirrectas, el vértice, el origen común de ambas.

Se designan de tres formas:

a.- Por sus lados y vértice, coronados por un sombrerete, en forma de acento circunflejo AÔB.

b.- Por su vértice, con el sombrerete ô.

c.- Por letras griegas α, β, δ. FIG. 13

Ø    UNIDADES: Los ángulos se miden por los arcos denominada grado, se divide un cuarto de circunferencia en un número determinado de partes iguales:

1. Sistema Sexagesimal.- La circunferencia completa tiene 360º. Un grado se divide a su vez en 60 minutos (60’), y estos en 60 segundos (60‘’) por lo que un grado tiene 3600’’.

2. Sistema Centesimal.- Si dividimos el cuarto de circunferencia en 100 partes. Un grado (1^g) se divide a su vez, en este sistema, en 100 minutos (100^m) y estos en 100 segundos (100^s) por lo que un grado tiene 10000^s. La circunferencia tiene 400^g y el ángulo recto 100^g.

Ø    TIPOS DE ÁNGULOS: Los ángulos pueden ser: Llanos, Convexos, Recto, Agudo, Obtuso, Cóncavos.

Ø    RELACIONES ENTRE ÁNGULOS:

1°) En función de la suma de ángulos.

- Complementarios: Dos ángulos son complementarios entre sí cuando entre los dos suman 90º o forman un ángulo recto.

- Suplementarios: Dos ángulos son suplementarios entre sí cuando entre los dos suman 180º o forman un ángulo llano.

2°) En función de la posición de sus lados.

- Consecutivos: Dos ángulos son consecutivos cuando tienen un lado común.

- Adyacentes: Dos ángulos son adyacentes cuando son consecutivos y sus lados no comunes forman un ángulo llano. Son adyacentes todos los suplementarios.

- Ángulos opuestos por el vértice:  Formados por dos rectas al cortarse, son iguales dos a dos..

 

 2.2) POLÍGONOS.

A) DEFINICIÓN.- Es la superficie plana limitada por una línea poligonal cerrada. Línea poligonal es la figura formada por varios segmentos no pertenecientes a la misma recta. Se considera cerrada cuando su principio y final coinciden.

B) ELEMENTOS:

-LADO: es cada uno de los segmentos que delimita la figura:                  

-VÉRTICE: punto de intersección de los lados:                             

-DIAGONAL: segmento que une dos vértices no consecutivos:                              

-ÁNGULO INTERIOR: es el ángulo que forman dos lados consecutivos: α, β, ρ, δ, ε .                                     

-ÁNGULO EXTERIOR: ángulo adyacente al ángulo interior: ζ, η, θ, μ, ϕ.

                                   

 

 

c) CLASIFICACIÓN DE LOS POLÍGONOS.

1°) SEGÚN EL NÚMERO DE LADOS: A partir de tres lados hasta veinte lados, tienen nombres específicos.

 

NOTA: Lo mejor es decir: “polígono de n lados” cuando el polígono tiene más de 20 lados.

 

2°) SEGÚN SUS ÁNGULOS: Dependiendo del ángulo que conforman los pares de lados consecutivos del polígono, se clasifican en: cóncavo o convexo.

a.- Polígonos cóncavos: Cuando contienen uno o más ángulos internos con medidas mayores que 180°, quiere decir que la concavidad se observa desde el exterior del polígono.

b.- Polígonos convexos: Cuando la medida de todos los ángulos internos, son menores de 180°, dando a entender que la convexidad se observa desde el exterior del polígono.

 

 

3°) SEGÚN LA IGUALDAD O DESIGUALDAD DE ÁNGULOS Y LADOS:

- POLÍGONOS REGULARES: Son aquellos que tienen lados iguales y ángulos iguales, es decir, son equiláteros y equiángulos. No todos los polígonos equiláteros son regulares, pero sí todos los polígonos regulares son equiláteros. No todos los polígonos equiángulos son regulares, pero sí todos los polígonos regulares son equiángulos.

 

- POLÍGONOS IRREGULARES: Son aquellos que tienen lados desiguales, ángulos desiguales o ambos.

Ejemplo:

 

NOTA: La única figura que a fuerza sí es equilátera, es equiángula y viceversa, … es el TRIÁNGULO EQUILÁTERO.

 

 

TERCERA PARTE:

3.1.- VIDEOS DE REFURZO: Ingresar a los siguientes links y analizar:

1º.- ELEMENTOS  BASICOS DE LA GEOMETRIA.

https://www.youtube.com/watch?v=jlu-b18RYsk

 

2°. – CLASIFICACIÓN DE LOS POLIGONOS.

https://www.youtube.com/watch?v=fobhsYGab40

 

 

CUARTA PARTE: Teniendo en cuenta lo leído y visualizado, resuelve lo siguiente:

ACTIVIDAD 1: CUESTIONARIO:

1.- ¿Cuáles son los elementos geométrico fundamentales?

2.- ¿Cuáles son los tipos de rectas?

3.- ¿Cuáles son los SUBTIPOS de rectas?

4.- ¿Qué es un ángulo?

5.- ¿En qué sistema se miden los ángulos?

6.- ¿Cuáles son los tipos de ángulos?

7.- ¿Cuál es la relación de los ángulos en función de la SUMA de sus ángulos?

8.- ¿Cuál es la relación de los ángulos en función de la POSICIÓN de sus lados?

9.- ¿Qué es un polígono?

10.- ¿Cuál es la clasificación de los polígonos según la IGUALDAD o DESIGUALDAD de sus ángulos y lados?

 

ACTIVIDAD 2: Completar la tabla, colocando los nombres de los polígonos según sus lados:

 

N° Lados	Polígono	N° Lados	Polígono
03		90
20		09
39		25
11		100
50		17

 

ACTIVIDAD 3: Dibujar 5 polígonos regulares.

 

 

QUINTA PARTE: Actividades de reflexión.

Después de haber realizado tu trabajo, reflexiona con tus compañeros respondiendo las siguientes preguntas:

¿Para qué nos son útiles determinar los elementos y propiedades de una figura geométrica?, ¿Podrías comentar en qué otras situaciones podemos utilizar dichos conocimientos?, ¿Qué elementos relevantes hemos reconocido en ellas?, ¿Qué dificultades encontraste y que hiciste para superarlas?, ¿por qué crees que algunos tienen una respuesta diferente?, ¿qué nociones relacionaste?, ¿cuáles fueron las que más encontraste?

 

SEXTA PARTE:

6.1.- RETO: Resolución de preguntas, dada por el docente en aula de acuerdo a la sesión desarrollada.

6.2.- ENTREGA: En físico, de manera presencial.

 

¡BUENA SUERTE¡

 

 

 

Vallejos MARRUFO, Elías.

PROFESOR

 

“No digas ¡cuando tenga tiempo estudiaré!, porque quizás nunca tendrás tiempo” (Hilel, Pirkei Avot)