MATERIAL SESION 3-P2-MAT.3º

 

MATERIAL DE LECTURA

PRIMERA PARTE: LECTURAS

PROPIEDADES DE LAS FIGURAS GEOMÉTRICAS.

I.- INTRODUCCION:

Las figuras geométricas componen todo lo que está alrededor de nosotros. Pueden ser BIDIMENSIONALES, como la pantalla de tu computadora, y TRIDIMENSIONALES, como una pelota.  Cada figura geométrica tiene sus propiedades que la hacen diferente de otras figuras. Sin embargo, las figuras geométricas pueden compartir propiedades con otras, lo que requiere describirlas más detalladamente para distinguirlas de otras figuras.

Las formas y figuras geométricas son aspectos que encontramos en nuestro andar cotidiano, el conocimiento de estas nos permite construir poco a poco el entorno que nos rodea, de manera inconsciente nos apropiamos de conocimientos informales acerca de estas y no es hasta que ingresamos a una institución formal que asimilamos y reconocemos las propiedades de cada una de ellas, que posteriormente nos permitirán realizar ejercicios más complejos con ellas.

Vamos a mencionar características y propiedades generales que tienen todas las figuras geométricas: tienen alto; largo y ancho; cada superficie se llama cara; Arista: cada línea recta entre dos caras; El punto donde se unen tres aristas se llama vértice.

1.1.- LADOS: El número de lados que tiene una figura puede ayudar a determinar qué tipo de figura geométrica es. Todas las figuras BIDIMENSIONALES hechas con líneas rectas se consideran polígonos.  Por ejemplo, un triángulo es una figura bidimensional que tiene tres lados. Los lados por sí solos no identifican la figura. Hay muchas figuras que tienen cuatro lados, como los cuadrados, rectángulos, rombos, trapezoides y muchas otras. Sin embargo, todas las figuras con cuatro lados se consideran cuadriláteros. Algunas figuras no tienen esquinas y por lo tanto no tienen lados distinguibles. Los círculos y los óvalos son ejemplos de figuras geométricas que no tienen lados distinguibles.

1.2.- ANGULOS: Las figuras que tienen esquinas, también llamadas vértices, crean ángulos que pueden medirse. Los ángulos están presentes tanto en las figuras Bidimensionales como en las Tridimensionales. Un ángulo puede medirse usando un transportador. Un ángulo puede ser agudo, lo que significa que mide menos de 90 grados, recto, que quiere decir que es de exactamente 90 grados, u obtuso, lo que significa que es mayor a 90 grados.

1.3.- FIGURAS GEOMÉTRICAS REGULARES E IRREGULARES: Las figuras Bidimensionales pueden clasificarse en regulares e irregulares. Los polígonos regulares son polígonos cuyos lados y ángulos interiores son congruentes, es decir, iguales. Un triángulo equilátero es un triángulo en el que los tres lados son iguales en longitud y todos los ángulos interiores son de 60 grados, lo que lo hace un triángulo regular. No todas las figuras pueden ser regulares. Un rectángulo, por ejemplo, por definición tiene dos lados que son iguales en longitud. Un lado es más largo que el otro. Esto hace que el rectángulo sea una figura irregular.

1.4.- FIGURAS GEOMÉTRICAS TRIDIMENSIONALES: La geometría no se limita a las figuras Bidimensionales. También incluye las figuras tridimensionales, llamadas también figuras sólidas. Estas figuras tienen un valor adicional de profundidad que no tienen las figuras bidimensionales. Las figuras tridimensionales se construyen con figuras bidimensionales. Por ejemplo, un cubo es una figura tridimensional que se construye con seis cuadrados ordenados en la forma de una caja. Otras figuras son una combinación de varias figuras geométricas. Un prisma es una combinación de rectángulos y triángulos

1.5.- BASE: Las figuras tridimensionales tienen bases. La base es la cara de la figura que descansa sobre un plano. Por ejemplo, una pirámide tiene una base cuadrada. Un cilindro tiene una base circular. En algunos casos, la base es igual al resto de las caras, como en el caso de un cubo. Una esfera, que se ve como una pelota, no tiene una base. Una esfera se describe como una figura en la que todos los puntos están a la misma distancia del centro.

II.- PROPIEDADES GENERALES: Las Vamos a ver a continuación algunas de tantas figuras geométricas y sus propiedades.

2.1.- EL RECTANGULO:

1. Cuadrilátero en el que sus cuatro vértices forman ángulos rectos.

2. Los lados opuestos de un rectángulo tiene la misma longitud.

3. vértices: 1,2,3,4

4. Lados opuestos: misma longitud.

2.2.- EL TRIANGULO GENERAL:

1. Un lado de un triángulo es menor que la suma de los otros dos (a < b+c ) y mayor que su diferencia 

( a > b- c)

2. La suma de los ángulos interiores de un triángulo es igual a 180º:  A+B+C =180º

3. El valor de un ángulo exterior de un triángulo es igual a la suma de los dos interiores no adyacentes:

                                      α = A+ B                                                         α = 180º - C                    

4. En un triángulo a mayor lado se opone mayor ángulo.

5. Si un triángulo tiene dos lados iguales, sus ángulos opuestos también son iguales.

2.3.- EL TRIANGULO RECTANGULO:

1. Es aquel que en esquina tiene un ángulo recto que mide 90º

2. Angulo recto es el vértice “A”.

4. El ángulo B y C suman 90º (ángulo recto)

5. Si se unen al lado opuesto dos triángulos similares se forma un rectángulo.

 

2.4.- EL CUADRADO:

1. Cuadrilátero que en sus cuatro vértices se forman ángulos rectos y que los cuatro lados tienen la misma longitud.

2.- Área del cuadrado: A = L²

 2.5.- EL ROMBO:

1. Los cuatro lados son iguales.

2. Los pares de ángulos opuestos son iguales.

3. Cada dos ángulos contiguos son suplementarios (suman 180º).

4. Sus dos diagonales se cortan en sus puntos medios.

5. Sus dos diagonales 5on perpendiculares (forman un ángulo de 90º).

6. Cada diagonal es bisectriz de los ángulos cuyos vértices une (los divide en partes iguales).

2.6.- EL TRAPECIO:

1. El segmento que une los puntos medios de sus diagonales es paralela a las bases del trapecio y mide la diferencia de las bases.

2. Un trapecio, no rectángulo, puede descomponerse en dos triángulos rectángulos y un rectángulo mediante alturas trazadas de los extremos de la base menor a la base mayor.

3. Si los lados de un trapecio son respectivamente iguales a los de otro trapecio, los trapecios son iguales.

4. Para que un trapecio sea isósceles es necesario y suficiente que los ángulos en la base sean iguales o alternativamente las diagonales sean iguales.

5. Las bisectrices de los ángulos adyacentes de un lado lateral forman un ángulo recto y se intersecan en un punto situado en la mediana del trapecio.

6. Sobre un paralelogramo, a partir de dos vértices opuestos, sobre los lados paralelos tome sendos puntos equidistantes, luego cuando se los une mediante un segmento, se determinan dos trapecios complementarios e iguales. Esto es, todo paralelogramo se puede descomponer en dos trapecios iguales.

7. Todo trapecio isósceles se puede descomponer en dos trapecios rectángulos iguales, mediante un segmento que une los putos medios de las bases

8. La recta que contiene al segmento es eje de simetría de las figuras resultantes.

9.- Área del trapecio: (base mayor + base menor) x altura entre 2

 2.7.- POLIGONOS REGULARES:

1.- PROPIEDAD FUNDAMENTAL: En todos los polígonos regulares, el trazado de sus radios los divide en tantos triángulos como lados posean; cuyas alturas son iguales al apotema del polígono, y cuyas bases sumadas son iguales al perímetro del polígono.

2.- En consecuencia, la superficie de un polígono regular será igual a la suma de las superficies de los triángulos que lo forman. Extendiendo la fórmula de cálculo de la superficie del triángulo, se deduce:

A = (perímetro x Apotema) : 2

3. Un polígono con “n” lados, tienen como suma de sus ángulos interiores 180º (n- 2)

4. La suma de los ángulos exteriores de un polígono es igual a 360º

5. La suma de los ángulos interiores y exterior de un vértice del polígono es de 180º.

6. La suma de los ángulos interiores y exteriores del polígonos es 180º n.

7.- Como la medida de la suma de todos los ángulos que pueden formarse alrededor de un punto es de 360° la medida del ángulo central de un polígono regular es igual a 360º dividido por la cantidad de lados.

Ejemplo:

-Ángulo central del triángulo equilátero: 360°: 3 = 120°.

-Ángulo central del cuadrado: 360° : 4 = 90°.

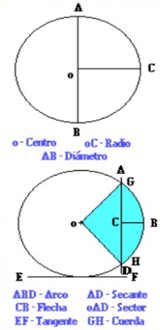
2.8.- EL CIRCULO:

1. El perímetro de un circulo es una circunferencia.

2. El Área del circulo: A = π. r²

-El Área del circulo como superficie interior del polígono de infinitos lados.

- El área de un circulo se deduce sabiendo que la superficie interior de cualquier polígono regular es igual al producto entre el  apotema y el perímetro de este polígono.

-Área del circulo como superficie triangular.

- Si en un círculo desplegamos todos sus anillos circulares, y los consideramos como rectángulos, se forma un triángulo rectángulo de altura “r” y base 2π.r (siendo la longitud de la base la de la circunferencia perimetral).

3. Semicírculo:

-Es la mitad de un circulo.

- Es la figura geométrica plana (bidimensional) de limitada por un diámetro y la mitad de una circunferencia.

-Su área es la mitad de la del círculo.

-El arco de un semicírculo siempre mide 180º, por ser la mitad de los 360º de un circulo.

4.- La propiedad fundamental del círculo, consiste en que existe una relación permanente entre su radio y la medida de su circunferencia, que es un valor constante de 3,1416; el cual se designa con la letra “π”.

SEGUNDA PARTE:

Visualizar los siguientes videos:

1.- https://www.youtube.com/watch?v=ZPwkPKbD71A&ab_channel=GabrielBucio-Matem%C3%A1ticasdesdeceroGabrielBucio-Matem%C3%A1ticasdesdecero

2.- https://www.youtube.com/watch?v=ElTqHb4ulLM&ab_channel=Mtra.YAQUELINASTORGAMtra.YAQUELINASTORGA

 

TERCERA PARTE: Responder a las siguientes preguntas:

1.- ¿Es igual una figura geométrica con un cuerpo geométrico? Explica.

2.- ¿De qué forma pueden ser las figuras geométricas?

3.- ¿Cómo se les llama a las figuras geométricas TRIDIMENSIONALES?

4.- ¿Cuáles son las características o propiedades principales de las figuras geométricas BIDIMENSIONALES? Da tres ejemplos:

5.- ¿Cuáles son las características o propiedades principales de las figuras geométricas TRIDIMENSIONALES? Da tres ejemplos:

6.- ¿De dónde nacen las figuras geométricas TRIDIMENSIONALES?

7.- ¿Cuál de las siguientes opciones presenta un cuerpo geométrico que tiene 4 Caras iguales?

8.- ¿Cuál de las siguientes opciones presenta un cuerpo geométrico que tiene 6 vértices?

9.- ¿Cuál de las siguientes opciones presenta un cuerpo geométrico que tiene 12 aristas?

CUARTA PARTE: RETO

1.- Elige la figura geométrica o cuerpo geométrico, que permita representar los instrumentos para moler alimentos.

2.- Representa tu trabajo, en una tabla de doble entrada, señalando:

a) El instrumento.

b) La figura que representa.

c) Sus propiedades.

 

QUINTA PARTE: Visitar el blog: saelmatematico.blogspot.com,

 

¡BUENA SUERTE!

 

 

......................................................

Vallejos MARRUFO, Elías.

PROFESOR

 

  

 

 

 

“Educar es más que dar carrera para vivir, es templar el alma para las dificultades y para soportar las injusticias” –PITÁGORAS

MATERIAL SESION 2-P2-MAT.3º

 

“Año del Bicentenario del Perú: 200 años de independencia” 

MATERIAL DE LECTURA

SESION Nº1-P2-3º-MATEMATICA

PRIMERA PARTE: LECTURAS

I.- GRÁFICOS ESTADÍSTICOS

Un gráfico estadístico es una representación visual de una serie de datos estadísticos. Es una herramienta muy eficaz, ya que un buen gráfico: capta la atención del lector; presenta la información de forma sencilla, clara y precisa; no induce a error; facilita la comparación de datos y destaca las tendencias y las diferencias; ilustra el mensaje, tema o trama del texto al que acompaña.

II.- TIPOS DE DATOS:

Las representaciones gráficas deben conseguir que un simple análisis visual ofrezca la mayor información y cómo los datos obtenidos se pueden representar a través de los gráficos. 

Según sea la variable, los gráficos más utilizados son:

2.1.- CUALITATIVOS: Se refieren a cualidades o modalidades que no pueden expresarse numéricamente. Pueden ser:

• ORDINALES: si siguen un orden o secuencia (ej. el abecedario, los meses del año).

• CATEGÓRICOS: si no siguen ningún orden (ej. el estado civil de las personas: solteros, casados, viudos, divorciados y separados).

2.2.- CUANTITATIVOS: se refieren a cantidades o valores numéricos. Pueden ser:

• DISCRETOS: si toman valores enteros (0, 1, 2, 3...). Ej. el número de hijos, el número de alumnos de una clase…

• CONTINUOS: si pueden tomar cualquier valor dentro de un intervalo (ej. la estatura o el peso de las personas).

III.- DIAGRAMAS DE BARRAS. Es una representación gráfica, en un eje cartesiano, de las frecuencias de variables CUALITATIVAS o de una CUANTITATIVA O DISCRETA (otorga cifras que se encuentran separadas en escalas, es decir que no poseen valores entre ellas, sino que el resultado comprende un valor exacto). Este gráfico, permite realzar la mayoría de gráficos estadísticos.

NOTA:

1º) Una variable CUALITATIVA, es un tipo de variable estadística que describe las cualidades, circunstancias o características de un objeto o persona, sin hacer uso de números y son: nominal y ordinaria o binaria.

2º) Las variables CUANTITATIVAS, son aquellas variables estadísticas que otorgan, como resultado, un valor numérico y son: discretas y continuas.

3.1.- UBICACIÓN DE LAS VARIABLES: En uno de los ejes, se posicionan las distintas categorías o modalidades de la variable cualitativa o discreta (en el ejemplo, el tipo de cereal) y en el otro el valor o frecuencia de cada categoría en una determinada escala (en el ejemplo, la producción en millones de toneladas de granos).

Ejemplo 1:

3.2.- ORIENTACION DE LAS BARRAS: La orientación del gráfico puede ser:

• VERTICAL: las distintas categorías están situadas en el eje horizontal y las barras de frecuencias crecen verticalmente.

• HORIZONTAL: las categorías se sitúan en el eje vertical y las barras crecen horizontalmente. Suelen usarse cuando hay muchas categorías o sus nombres son demasiado largos.

Las categorías pueden ordenarse alfabéticamente facilitando su búsqueda o por sus frecuencias facilitando la comparación de los datos.

EJEMPLO: El porcentaje de habitantes usuarios de internet del año 2007 por países (Fuente: Unión Internacional de Telecomunicaciones).

3.3.- SU USO: Se suelen usar para:

3.3.1.- Comparar magnitudes de varias categorías. Ejemplo: Fuente: Organización de las Naciones Unidas para la Agricultura y la Alimentación (FAO)

3.3.2.- Ver la evolución en el tiempo de una magnitud concreta. Ejemplo: Fuente: Organización de las Naciones Unidas para la Agricultura y la Alimentación (FAO)

3.4.- TIPOS DE GRÁFICOS DE BARRAS:

3.4.1.- SENCILLO: Contiene una única serie de datos. Ejemplo:

3.4.2.- AGRUPADO: Contiene varias series de datos y cada una se representa por un tipo de barra de un mismo color o textura. Ejemplo:

3.4.3.- APILADO: Contiene varias series de datos. La barra se divide en segmentos de diferentes colores o texturas y cada uno de ellos representa una serie. Ejemplo:

IV.- GRAFICO DE LINEAS:

4.1.- DEFINICION: Un gráfico de líneas, es una representación gráfica en un eje cartesiano de la relación que existe entre dos variables reflejando con claridad los cambios producidos. Pueden aparecer varias variables para compararlas.

Ejemplo 1:

Ejemplo 2: Fuente: Encuesta de Población Activa. INE

4.2.- CASO PARTICULAR 1: Es el POLIGONO DE FRECUENCIA, que se obtiene al unir los extremos superiores de las barras con una línea poligonal.

Ejemplo 1:

Las notas obtenidas por un grupo de alumnos en una prueba de matemáticas vienen resumida en la siguiente tabla:

Ejemplo 2:

4.3.- CASO PARTICULAR 2: Las pirámides de población se pueden presentar como un gráfico de líneas. Es útil cuando se quieren presentar varias series de datos, por ejemplo, si se quieren comparar pirámides de varios países, ver la población extranjera o comparar la estructura de población de varios años.

Ejemplo:

V.- HISTOGRAMAS:

5.1.- HISTOGRAMA NORMAL.- Se usa para representar las frecuencias de una variable cuantitativa continua o agrupadas en intervalos. En uno de los ejes se posicionan las clases de la variable continua (los intervalos o las marcas de clase que son los puntos medios de cada intervalo) y en el otro eje las frecuencias. No existe separación entre las barras. Los histogramas permiten compara datos de una forma rápida (basta mirar la gráfica)

El polígono de frecuencias se obtiene uniendo los puntos medios de las bases superiores de los 

rectángulos.

Ejemplo 1: El peso de un grupo de alumnos aparece recogido en la siguiente tabla:

Ejemplo 2:

5.2.- HISTOGRAMA BIDIRECCIONAL. - Tiene orientación horizontal y contiene dos series de datos cuyas barras de frecuencias crecen en sentidos opuestos. Las más comunes son las pirámides de población de las que hablaremos más adelante.

Ejemplo:

VI.- PIRÁMIDE DE POBLACIÓN. - Es un histograma BI-DIRECCIONAL que muestra la estructura demográfica de una población, por sexo y edad, en un momento determinado. En el eje vertical se posicionan los rangos de edades y en el horizontal los porcentajes de población. En una de las direcciones se colocan las barras que representan la distribución (% sobre el total de población) por edad de los varones y en la otra la distribución por edad de las mujeres.

Estos gráficos nos dan una visión de la juventud, madurez o vejez de una población y, por tanto, su grado de desarrollo.

Ejemplo 1:

Ejemplo 2: Edades de hombres y mujeres.

SEGÚN SU FORMA: Puede haber distintos tipos de pirámides:

• Pirámide de población PROGRESIVA: Existe un alto porcentaje de población joven que va desapareciendo según avanzan las edades. Son típicas de países subdesarrollados cuya esperanza de vida es baja y la tasa de natalidad alta. Ejemplo:

• Pirámide de población REGRESIVA: En la base existe menos población que en el medio y la población envejecida es considerable. Son típicas de países desarrollados cuya natalidad está descendiendo y la esperanza de vida es alta. Ejemplo:

• Pirámide de población ESTANCADA: Los tramos intermedios de edades tienen la misma población que la base. Son típicas de países en vías de desarrollo donde se ha controlado la mortalidad y se empieza a controlar la natalidad. Ejemplo:

VII.- GRÁFICO DE PARETO: Es un tipo de gráfico de barras vertical, ordenado por frecuencias de forma descendente que identifica y da un orden de prioridad a los datos. Ejemplo.

VIII.- DIAGRAMA DE SECTORES. Es una representación circular de las frecuencias relativas de una variable cualitativa o discreta que permite, de una manera sencilla y rápida, su comparación.

Es un gráfico empleado fundamentalmente para variables cualitativas.  Son útiles cuando las categorías son pocas. Si el gráfico tuviera muchas variables, no aportaría casi información y sería prácticamente incomprensible.

Las modalidades, se representan en un círculo dividido en sectores y la amplitud de cada sector medido en grados, que se obtiene multiplicando la frecuencia relativa por 360º.

Ejemplo 1: 

Un estudio hecho entre 100 alumnos universitarios, elegidos al azar sobre  el número de días a la semana que practican alguna actividad física viene dada por  la siguiente tabla:

Ejemplo 2:

IX.- PICTOGRAMAS.

Son gráficos que se representan mediante figuras o símbolos, las frecuencias de una variable cualitativa o discreta. Al igual que los gráficos de barras suelen usarse para comparar magnitudes o ver la evolución en el tiempo de una categoría concreta.

Su tamaño es proporcional a la frecuencia que representan.

Ejemplo 1:

Número de partidos ganados, perdidos o  empatados de un equipo.

Ejemplo 2:

X.- GRÁFICO DE DISPERSIÓN: Muestra en un eje cartesiano la relación que existe entre dos variables.

Ejemplo 1:

Ejemplo 2:

XI.- CARTOGRAMAS.

Un cartograma es un mapa en el que se presentan datos estadísticos por regiones, bien poniendo el número o coloreando las distintas zonas en función del dato que representan.

Ejemplo: Urbanización en el mundo atendiendo a la industrialización.

XII.- CLIMATOGRAMA:

Es un caso particular de aplicación de los histogramas y los polígonos de frecuencias, que representa la marcha anual de las temperaturas y de las lluvias, sobre un mismo sistema de coordenadas.

Ejemplo:

SEGUNDA PARTE:

Visualizar los siguientes videos:

1.-  https://www.youtube.com/watch?v=J-lDNbXM2wE&ab_channel=WissenSyncWissenSync

2.- https://www.youtube.com/watch?v=XFjDGydsGvU

3.-  https://www.youtube.com/watch?v=QomQP9_UZsA&ab_channel=LuisRinc%C3%B3nLuisRinc%C3%B3n

 

TERCERA PARTE: Responder a las siguientes preguntas:

1.- ¿Qué son gráficos estadísticos?

2.- ¿De qué depende usar un determinado gráfico estadístico?

3.- ¿Cuáles son los tipos de gráficos estadísticos?

4.- ¿Cuál es el grafico estadístico más usado en todos?

5.- ¿Cómo nace un POLIGONO de frecuencia?

6.- ¿Cuál es el nombre del video 1º? Explica el ¿por qué?

7.- ¿Cuál es el nombre del video 2º? Explica el ¿Por qué?

8.- ¿Cuál es el nombre del video 3º? Explica el ¿Por qué?

9.- ¿Cómo nace un POLIGONO de frecuencia?

 

CUARTA PARTE: RETO

1.- ¿Qué gráfico estadístico se adapta a tu trabajo realizado en la sesión Nº01-P2? ¿Por qué?

2.- Representa tu trabajo de la sesión Nº1-P2, en el Gráfico Estadístico seleccionado.