“Año del Fortalecimiento
de la soberanía nacional”
MATERIAL DE LECTURA-S8-3°G-P1-22
PRIMERA PARTE:
1.1.- DENOMINACION DE LA SESION 8:
“Conocemos con
alegría las unidades de tiempo, temperatura y monetaria”.
1.2.- PROPOSITO DE LA SESION 8:
ESTABLECER relaciones entre unidades de tiempo, de temperatura y monetaria.
1.3.- SITUACION SIGNIFICATIVA.
NAYELI, alumna del 3°Grado de secundaria de la I.E “San Carlos
de Monsefú, anuncia con ALEGRÍA que
celebrara su cumpleaños por haber cumplido 10 años 60 meses 146 días. Pero está
MOLESTA por haber comprado un pavo
con cinco billetes de 20, cuatro billetes de 10, tres monedas de 5, dos monedas de 2 y un sol. Además,
esta PREOCUPADA, ya que tiene que
colocar el pavo en la parrilla cuando alcance una temperatura de 374°F.
Nos preguntamos:
a) ¿Cuántos años cumple NAYELI?
b) ¿Cuánto le costó el pavo?
c) ¿A qué temperatura debe NAYELI fijar el graduador para asar el Pavo, si la
graduación está en grados centígrados (°C)?
SEGUNDA PARTE: LECTURAS.
2.1.- UNIDADES DE MEDIDA:
Una unidad de medida es
una cantidad estandarizada de una determinada magnitud física,
definida y adoptada por convención o por ley. Cualquier valor de una cantidad
física, puede expresarse como un múltiplo de la unidad de medida.
Una
unidad de medida toma su valor a partir de un patrón o
de una composición de otras unidades definidas previamente. Las primeras
unidades se conocen como unidades básicas o de base (fundamentales), mientras que las segundas se llaman unidades
derivadas.
Un
conjunto de unidades de medida en el que ninguna magnitud tenga
más de una unidad asociada es denominado sistema de unidades. Todas
las unidades denotan cantidades escalares.
2.2.- UNIDADES DE TIEMPO:
Las medidas de tiempo, son
aquellas unidades que utilizamos para medir períodos y el instrumento
que utilizamos para medir el tiempo es el reloj. La unidad que
utilizaremos como referencia será el día.
Con respecto al
día, hay unidades de tiempo menores y mayores que el día y su unidad fundamental es el segundo (s).
1°.- Periodos hasta un día
Minuto (min) = 60 s.
Hora (h) = 60 min = 3 600 s.
El día tiene 24 h.
1 hora (h) tiene 60 minutos
(min)
1 cuarto de hora: 15 minutos.
Media hora: 30 minutos.
3 cuartos de hora: 45 minutos
2.- Periodos superiores al día
Semana = 7 días.
Quincena = 15 días.
1 mes son 30 / 31 días
(febrero tiene 28 días, y cada 4 años tiene 29 días)
Trimestre = 3 meses.
Semestre = 6 meses.
1 año tiene 12 meses / 365
días (cada 4 años tiene un día más en febrero, con lo que son 366 días; se le
llama año bisiesto)
Bienio = 2 años.
Trienio = 3 años.
Lustro = 5 años.
Década = 10 años.
Siglo = 100 años.
Milenio = 1000 años.
Era = Muchos milenios (sin cantidad fija)
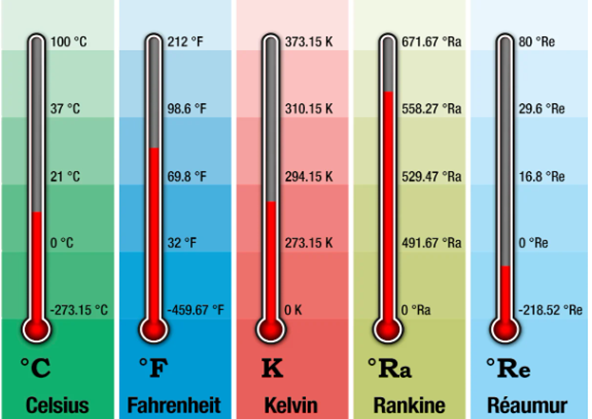
2.3.- UNIDADES DE TEMPERATURA:
En el sistema
internacional de unidades, la unidad de temperatura es el Kelvin (K), y el punto de inicio de la escala Kelvin (y
también para la escala de Rankine) es el cero absoluto correspondiente
a -273,15°C (grados Celsius o centígrados) igual a 0°K (grados Kelvin), o
bien -459,67°F (grados Fahrenheit) que es la temperatura más baja posible que puede
existir.
La escala más utilizada es la escala CELSIUS que
mide en grados centígrados, aunque en Estados Unidos se utiliza
preferentemente la escala FAHRENHEIT.
2.3.1.- COMPARACIONES:
2.3.2.- CONVERSIONES ENTRE UNIDADES DE
TEMPERATURA.
2.3.- UNIDADES MONETARIA:
Se describe como unidad monetaria a
la moneda oficial que
se encuentra vigente y circulando en una nación o país en específico, está en tierras
extranjeras es canjeable por oro o divisas. Siendo la base principal que
sostiene la economía de una nación;
la principal condición que debe cumplir es que debe ser distribuida según sus
diferentes fracciones, por lo tanto una moneda no debe tener un valor ni muy
alto ni muy bajo, debido a que el número de billetes variará según esta
regla.
2.3.1.- SISTEMA MONETARIO DEL PERU:
En
nuestra patria, la unidad Monetaria anteriormente se denominaba “Nuevo Sol” y hoy en día es “SOL” y su símbolo es S/. EI Sol es una moneda
plateada de 27 mm de diámetro y fracciones; así como, billetes de diferente
denominación:
TERCERA PARTE:
3.1.- VIDEOS DE REFURZO: Ingresar a los siguientes links y analizar:
1º.- UNIDADES DE TIEMPO.
https://www.youtube.com/watch?v=8xx1osFk_Dw
2°. – UNIDADES DE TEMPERATURA.
https://www.youtube.com/watch?v=8mp_f5hYxNI
3°. – UNIDADES MONETARIAS.
https://www.youtube.com/watch?v=t0qbWSaog9I
CUARTA PARTE: Teniendo en cuenta lo leído y visualizado, resuelve lo
siguiente:
4.1.- CUESTIONARIO:
1°) ¿Qué son unidades de tiempo?
2°) ¿Cuáles son las unidades
de temperatura?
3°) ¿Cuáles son las unidades
monetarias
5°) ¿Cuáles son las unidades
básicas del tiempo, temperatura y monetaria?
4.2.- EJERCICIOS DE APLICACION:
4.2.1- SOBRE UNIDADES
DE TIEMPO:
1°) Calcula la siguiente diferencia: 6h 13 min 24 s – 2h 24min
36 s:
2°) En una “BICICLETEADA CARLINA”, el ganador del TERCER GRADO recorrió dos tramos en los siguientes tiempos: 2 min 22 s y 3 min 45 s. ¿Cuánto tiempo empleó para llegar desde la salida a la meta?
3°) Cuando NAYELI llegó al aeropuerto miró su reloj y eran las 5:45 a.m., quedaban justo 3 horas para que despegase su vuelo a ROMA. Si el vuelo salió puntual y duró exactamente 114 minutos, ¿qué hora marcaba su reloj cuando aterrizó en ROMA?
4.2.2.- PROBLEMAS SOBRE TEMPERATURA:
1.- Si la temperatura del
cuerpo humano es en promedio 37°C. Expresarla en grados FAHRENHET.
2.- Un paciente llega a la posta médica de Monsefú diciendo, que tiene una temperatura corporal de 98,6 °F . Si en el Perú se mide en °C ¿Cuál es la temperatura del paciente?
4.2.3.- SOBRE UNIDADES MONETARIAS.
EJERCICOS:
Ejemplo 1:
¿Cuántos billetes de S/.20,00 hay en S/. 150,00?
Ejemplo 2: 60 monedas de S/. 0,10 + 20 monedas de S/. 0,20 ¿A cuántos nuevos soles equivalen?
Ejemplo 3: A un obrero le pagan por su trabajo semanal, con 2 billetes de S/. 100,00, 3 billetes de S/. 50,00 y 8 monedas de S/. 5,00 ¿Cuánto le pagaron?
Ejemplo 4: Un alumno de tercer Grado de la I.E San Carlos de Monsefú, realiza unas compras y paga con 4 monedas de S/. 5,00 c/u, 6 monedas de S/. 2,00 cada una y 4 billetes de S/. 10,00. ¿Cuánto pagó?
Ejemplo 4: Una madre de familia tiene 5 billetes de S/. 100 y 5 billetes de S/. 50 . Gasta en movilidad S/. 78,59 ; en dar un gustito con golosinas a su hijo de 8 años S/. 27,98 y en compras para la semana S/. 499,80, ¿cuánto le queda?
QUINTA PARTE: Actividades de reflexión.
Después de haber realizado tu trabajo,
reflexiona con tus compañeros respondiendo las siguientes preguntas:
¿Para qué nos son útiles determinar una unidad de tiempo,
temperatura y monetaria?, ¿Podrían comentar en qué otras situaciones podemos
utilizar dichos conocimientos?, ¿Cómo hemos identificado dichas unidades?,¿Qué
elementos relevantes hemos reconocido en ellas? , ¿Qué dificultades encontraste y que hiciste
para superarlas?, ¿por qué crees que algunos tienen una respuesta diferente?,
¿qué nociones relacionaste?, ¿cuáles fueron las que más encontraste?
SEXTA PARTE:
5.1.- RETO: Completar la tabla, dada por el docente
en aula de acuerdo a la sesión desarrollada.
5.2.- ENTREGA: En
físico, de manera presencial.
¡
BUENA SUERTE ¡
Vallejos MARRUFO, Elías.
PROFESOR
“No digas ¡cuando tenga tiempo
estudiaré!, porque quizás nunca tendrás tiempo” (Hilel, Pirkei Avot 2:6).