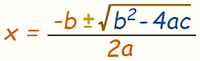“Año del Fortalecimiento de la soberanía nacional”
MATERIAL DE LECTURA-S4-P4-3°G-22
PRIMERA PARTE:
1.1.- DENOMINACION DE LA SESION 4:
“Observamos la función
de un emprendimiento social”
1.2.- PROPOSITO DE LA SESION 4:
Al finalizar la SESIÓN 4, el estudiante del TERCER
GRADO de secundaria, RESOLVERÁ ECUACIONES
CUADRÁTICAS, usando productos notables o propiedades de las igualdades.
1.3.- SITUACION SIGNIFICATIVA.
Un alumno muy Emprendedor,
de la I.E “San Carlos” del distrito de Monsefú, se ha dedicado a la comercialización
de “Artesanía” por delivery, su ganancia esta dado por: G(x) = 5x2 + 10x + 400
Donde “x” es la cantidad (en decenas) de artesanía que fabrica. Se
pregunta: ¿Qué cantidad debo
vender para tener un máximo beneficio? Y ¿Cuál sería mi máxima ganancia?
Como alumnos, del Tercer Grado: ¿Podrías ayudarle?, ¿De qué manera?
SEGUNDA PARTE: LECTURAS.
2.1.- LA FUNCION CUADRATICA:
2.1.1.- DEFINICIÓN:
Una función
cuadrática (o parabólica) es una función
polinómica de segundo grado. Es decir, tiene la forma: f(x) = ax2
+ bx + c ; siendo a ≠ 0
Esta forma de escribir la
función se denomina forma general.
FORMA: La gráfica de una
función cuadrática siempre es una parábola.
ORIENTACION: Las parábolas
tienen forma de ∪ (si a > 0) o de ∩ (si a < 0).
AMPLITUD: Además de la
orientación, el coeficiente “a” es la causa de
la amplitud de la función: cuanto mayor es |a|, más rápido crece (o decrece) la parábola, por lo que es más cerrada.
EJEMPLO.
2.1.2.- VERTICES:
Las FUNCIONES
CUADRÁTICAS tienen un máximo (si a < 0) o un mínimo (si a > 0). Este punto es el vértice de
la parábola; por lo que, la primera coordenada del vértice es:
Y la segunda coordenada es su IMAGEN:
EJEMPLO 1: Calcular el vértice de la función: f(x) = -2x2 + 3x
SOLUCION
1°) Identificamos los coeficientes: a = -2
; b = 3 ; c =
0
2°) ORIENTACION: Como valor de “a” es negativo, la parábola tiene forma
de ∩. El vértice es un máximo.
3°) VERTICES:
Entonces la primera coordenada del vértice es:
Calculamos la segunda coordenada, reemplazando en: f(x) = -2x2 + 3x
Por tanto, el VÉRTICE es el punto:
4°) GRÁFICA:
2.1.3.- PUNTOS DE CORTE CON LOS EJES:
Una
parábola siempre corta el EJE DE ORDENADAS (eje
Y) en un punto. Como esto ocurre cuando “x = 0”, se trata del punto (0 , c) puesto
que: f(0) = c.
Una
función corta al EJE DE ABSCISAS (eje X)
cuando y = 0. Por tanto, para hallar estos puntos de
corte, tenemos que resolver una ecuación cuadrática: ax2 + bx + c = 0
Como una ecuación cuadrática
puede tener una, dos o ninguna solución, puede haber uno, dos o ningún punto de
corte con el eje X.
Recordamos la fórmula que
necesitamos:
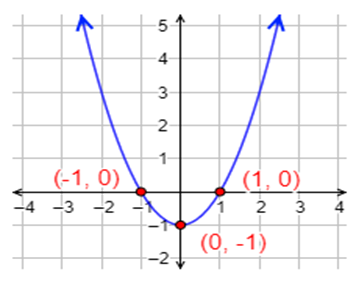
EJEMPLO 2: Calcular los PUNTOS DE CORTE de la función: f(x) = x2 – 1
SOLUCION
1°) Los coeficientes de la ecuación son: a = 1 ; b = 0 ; c = −1
2°) PUNTO DE CORTES:
Eje Y: (0 , c)
El punto de corte con el eje Y
es (0,−1)
Eje X: y = 0
Resolvemos aplicando la
fórmula, la ecuación de segundo grado: x2
– 1 = 0
Hay dos soluciones: x = 1 y x = −1
La segunda coordenada es “0” , por tanto, tenemos los puntos de corte: (1 , 0) , ( -1 , 0)
TERCERA PARTE:
VIDEOS DE REFURZO: Ingresar a los siguientes links y analizar:
3.1.- Gráfica de la función cuadrática o de segundo grado.
https://www.youtube.com/watch?v=6JQw45YO3Fs
CUARTA PARTE: Teniendo en cuenta lo leído y visualizado, resuelve lo
siguiente:
I.- En una empresa han
hecho un estudio sobre la rentabilidad de su inversión en publicidad, y han
llegado a la conclusión de que el BENEFICIO obtenido, en miles de Soles, viene
dado por la expresión B(x)=0,5x2-4x+6, siendo “x” la inversión en
publicidad, en miles de Soles, con x en el intervalo [0,10]
a) ¿Para qué valores de la inversión la empresa
tiene pérdidas?
b) ¿Cuánto tiene que invertir la empresa en
publicidad para obtener el mayor beneficio
posible?
c) ¿Cuál es el beneficio si no se invierte nada en publicidad?
d) ¿Hay algún otro valor de la inversión para el cual se obtiene el mismo beneficio?
II.- El Beneficio (en miles de Soles) que obtiene una central lechera por la producción de leche, está determinada por la función: B(x) = -x2 + 7x - 10 Donde “x” representa los hectolitros producidos en una semana.
a.-
¿Cuántos hectolitros debe producir para maximizar el beneficio?
b.- Calcular el beneficio Máximo.
III.- La ganancia G (en millones de Soles), en una empresa dedicada a la comercialización
de autos está dada por: G(x) = -7500 + 200x – x2
Donde “x” es la cantidad (en decenas de autos) que la empresa fabrica:
a) ¿Qué cantidad deberá vender la empresa para
tener un máximo beneficio?
b) Encuentre la máxima ganancia.
IV.- El dueño de un comercio de artículos que sabe que si semanalmente vende “x” artículos, sus ganancias son: U = -2x2 + 40x + 280, desea determinar:
a) ¿Cuál es el número de unidades que deberá vender,
para que la utilidad sea máxima?
b) ¿Cuál es la unidad máxima?
¿calcula la cantidad de radios por fabricar, para que el costo sea el mínimo?
QUINTA PARTE: Actividades de reflexión.
Después de haber realizado tu trabajo,
reflexiona con tus compañeros respondiendo las siguientes preguntas:
¿Para qué nos son útiles aplicar las FUNCIONES CUADRATICAS?,
¿Podrías comentar en qué otras situaciones podemos utilizar dichos conocimientos?,
¿Cómo has identificado las variables a encontrar en la resolución de problemas?,¿Qué
elementos relevantes has reconocido en ellas? , ¿Qué dificultades encontraste y que hiciste para superarlas?, ¿por qué
crees que algunos tienen una respuesta diferente?, ¿qué nociones relacionaste?,
¿cuáles fueron las que más encontraste?
SEXTA PARTE:
6.1.- PRODUCTO: RESOLVER la situación significativa, tomando como referencia los conocimientos
aprendidos y compartidos en el aula de acuerdo a la sesión
desarrollada.
6.2.- ENTREGA: En físico, de manera presencial.
¡
BUENA SUERTE ¡
Vallejos MARRUFO, Elías.
PROFESOR
“No digas ¡cuando tenga tiempo
estudiaré!, porque quizás nunca tendrás tiempo” (Hilel, Pirkei Avot).