“Año del Fortalecimiento de la soberanía nacional”
MATERIAL DE LECTURA-S3-P4-3°G-22
PRIMERA PARTE:
1.1.- DENOMINACION DE LA SESION 3:
““Determinado el crecimiento de un emprendimiento
social”
1.2.- PROPOSITO DE LA SESION 3:
Al finalizar la SESIÓN 3, el estudiante del TERCER
GRADO de secundaria, RESOLVERÁ ECUACIONES
CUADRÁTICAS, usando productos notables o propiedades de las igualdades.
1.3.- SITUACION SIGNIFICATIVA.
Como alumnos del
Tercer Grado: ¿podría
ayudarle?, ¿De qué manera?
SEGUNDA PARTE: LECTURAS.
2.1.- ECUACION CUADRATICA:
2.1.1.- DEFINICIÓN:
2.1.2.- UTILIDAD DE UNA ECUACIÓN CUADRÁTICA:
Las ecuaciones cuadráticas, a veces se
usan para modelar situaciones o relaciones en los negocios, en la ciencia y en
la medicina. Un uso común en los negocios es maximizar las ganancias, es decir, la diferencia entre los ingresos
(dinero que entra) y los costos de
producción (dinero gastado).
La relación entre el costo de un
artículo y la cantidad vendida es normalmente lineal. En otras palabras, por
cada UN SOL de incremento en el precio hay un decremento correspondiente en la
cantidad vendida.
Por ejemplo: Si el precio de algo sube,
¿compras más o menos? ¡Esperemos
que menos!.
Una vez que, determinamos la relación
entre el precio de venta de un artículo y la cantidad vendida, podemos pensar
en cómo generar la máxima ganancia. ¿A qué precio
de venta haríamos más dinero?
La cantidad de ganancia se encontrará
tomando el total de ingresos (la cantidad
vendida multiplicada por el precio de venta) y restando el costo de
producir todos los artículos:
Ganancia = Ingreso Total – Costos de Producción.
Podemos integrar la relación lineal del
precio de venta a la cantidad y la fórmula de la Ganancia y
crear una ECUACIÓN CUADRÁTICA, que
entonces podemos maximizar.
2.1.3.- FORMA ESTÁNDAR DE UNA ECUACIÓN CUADRÁTICA:
Donde:
1°) “a”, “b” y “c” son
valores conocidos. “a” no puede ser 0.
2°) “x" es la variable o incógnita (todavía no sabemos su valor).
Ejemplo 1: 2x2 + 5x + 3 = 0
En esta: a = 2 ; b =
5 ;
c = 3
Ejemplo 2: x2 - 3 = 0
En esta: a = 1 ; b =
-3 ;
c = 0
Ejemplo 3: 5x - 9 = 0
En esta: ¡NO ES UNA ECUACIÓN CUADRÁTICA!, ¿Por qué? Porque
le falta: x2
2.1.4.- ECUACIONES CUADRÁTICAS DISFRAZADAS.
¡Pero a veces una
ecuación cuadrática se ve diferente! Por ejemplo:
2.1.5.- SOLUCIÓN DE UNA ECUACIONES CUADRÁTICAS.
Las "soluciones" de una
Ecuación Cuadrática son los valores donde la ecuación es igual a cero.
También se les llama "raíces",
o incluso "ceros". Normalmente
hay 2 soluciones (como se muestra en la
gráfica).
2.1.6.- MÉTODOS DE SOLUCIÓN DE UNA ECUACIÓN CUADRÁTICA.
Existen diferentes
métodos, para encontrar las soluciones:
1°) FACTORIZAR EL CATEDRÁTICO. (encontrar qué es lo que hay que multiplicar
para generar la ecuación cuadrática).
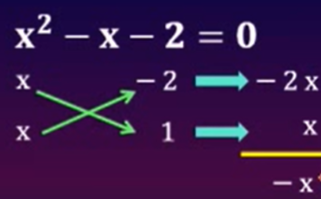
Ejemplo: Hallar el valor de “x” Factorizando: x2 - x - 2 = 0
SOLUCION:
Aplicando el método del
aspa.
Luego tenemos:
(x - 2) (x + 1) =0
X - 2 = 0
o x + 1 = 0
Luego: x = 2
o x = -1
Por lo tanto, las soluciones de la ecuación son: x = -2 y x = -3.
Ejemplo: Hallar el valor de “x” completando
cuadrados: x2 + 6x - 7 = 0
SOLUCION:
Sacamos la mitad del
coeficiente del segundo término, lo elevamos al cuadrado y luego completamos la
ecuación con su opuesto, para que la ecuación no sé altere:
6 : 2 = 3, entonces 32
= 9.
Luego: x2
+ 6x + 9 – 9 - 7 = 0
Los 3 primeros forman un trinomio cuadrado perfecto y lo
factorizamos:
x2 +
6x + 9 – 9 - 7 = 0
( x + 3)2 – 9 – 7
= 0
(x + 3)2 = 16
Sacamos raíz cuadrada a
ambos:
/x + 3/ = 4
Entonces tenemos:
x + 3 = 4
o x + 3 = - 4
x = 4 -
3 o x
= - 4 - 3
x = 1 o
x = - 7
3°) USANDO LA FÓRMULA
CUADRÁTICA:
DONDE:
1°)
2°) “b2 − 4ac” Se llama Discriminante,
porque puede "discriminar"
entre los posibles tipos de respuesta:
Ø Cuando “b2 − 4ac” es
positivo, obtenemos dos soluciones reales.
Ø Si “b2 − 4ac” es “cero”, sólo
hay UNA solución real (en realidad las
dos soluciones son la misma)
Ø Cuando “b2 − 4ac” es
negativo, obtenemos un par de soluciones complejas. Es
aquí cuando el "Discriminante" nos ayuda.
TERCERA PARTE:
VIDEOS DE REFURZO: Ingresar a los siguientes links y analizar:
3.1.- ECUACIÓN CUADRÁTICA.
https://www.youtube.com/watch?v=_bP6NowsO-Y
3.2.
– RESOLVIENDO ECUACIONES CUADRÁTICAS CON 4 MÉTODOS.
https://www.youtube.com/watch?v=BWzy9fJZO50
CUARTA PARTE: Teniendo en cuenta lo leído y visualizado, resuelve lo
siguiente:
I) Hallar el valor de “x” de las ecuaciones
cuadráticas, factorizando:
1.1.-
x2 + 5x + 6 = 0
a) -2 y -3 b) 2 y 3 c) 3 y 2 d) -3 y -2 e) N.A
1.2.- x2 + 2x – 8 = 0
a) -2 y -3 b) -4 y 2 c) 4 y -2
d) 4 y 2 e) N.A
1.3.- 2x2 −13x – 24 = 0
a) 3/2 y -8 b) 2 y 8 c) -3/2 y 8
d) 3/2 y 8 e) N.A
a) 3 y 5 b) -3 y -5 c) -3/2 y 8
d) -3 y 5 e) N.A
a) 3/2 y -8 b) 2 y 8 c) -3/2 y 8
d) 3/2 y 8 e) N.A
1.6.- 3x2 + 14x – 12 = 2x 2 + 15x
a) -3 y 4 b) 2 y 8 c) -3 y -4
d) 4 y -3 e) N.A
2.1.- 2x2 + 7x – 15 = 0
a) 7/4 y -7/4 b) 7 y 4 c) 4/7 y -4/7
d) 4 y 7 e) N.A
a) 3/2 y -8 b) -2 y -8 c) 2 y 8 d) -8 y -2 e) N.A
a) -4 y 0 b) 2 y 8 c) 0 y -4 d) 4 y -3 e) N.A
a) 323 y 1 b) 2 y 8 c) -3 y -4
d) 3,23 y 0,1 e) N.A
a) -16 y 0 b) 4 y 8 c) 8 y 4 d) 0 y -16 e) N.A
3.1.- x2 - 4x + 3 = 0
a) 3 y 1 b) 1 y 3 c) -1 y -3
d) -3 y -1 e) N.A
a) -3 y 4 b) 2 y -5 c) -5 y 2 d) -5 y -2 e) N.A
a) -3 y -1 b) -3 y 1 c) -3 y -4
d) 1 y -3 e) N.A
a) 3 y -2/3 b) 3 y 2/3 c) -3 y -2/3
d) 4 y -3 e) N.A
a) 3/2 b) 2 y 8 c) -3 y -4
d) -3/2 e) N.A
a) -3 y 4 b) 2 y 8 c) -3 y -4
d) 4 y -3 e) N.A
4.2.- TAREA: APLICAR LOS MÉTODOS DE SOLUCIÓN DE LAS ECUACIONES CUADRÁTICAS, DANDO LA RESPUESTA AL ALUMNO INNOVADOR DE LA SITUACION SIGNIFICATIVA.
QUINTA PARTE: Actividades de reflexión.
Después de haber realizado tu trabajo,
reflexiona con tus compañeros respondiendo las siguientes preguntas:
¿Para qué nos son útiles aplicar las ECUACIONES CUADRATICAS?,
¿Podrías comentar en qué otras situaciones podemos utilizar dichos
conocimientos?, ¿Cómo has identificado las variables a encontrar en la
resolución de problemas?,¿Qué elementos relevantes has reconocido en ellas? , ¿Qué dificultades encontraste y que hiciste
para superarlas?, ¿por qué crees que algunos tienen una respuesta diferente?,
¿qué nociones relacionaste?, ¿cuáles fueron las que más encontraste?
SEXTA PARTE:
6.1.- PRODUCTO: RESOLVER la situación significativa, tomando como referencia los conocimientos
aprendidos y compartidos en el aula de acuerdo a la sesión
desarrollada.
6.2.- ENTREGA: En físico, de manera presencial.
¡
BUENA SUERTE ¡
Vallejos MARRUFO, Elías.
PROFESOR
“No digas ¡cuando tenga tiempo
estudiaré!, porque quizás nunca tendrás tiempo” (Hilel, Pirkei Avot).







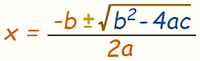





No hay comentarios:
Publicar un comentario