“Año del
Fortalecimiento de la soberanía nacional”
MATERIAL DE LECTURA
S5-P3-2022
PRIPRIMERA PARTE
2.2. 1.1.- DENOMINACIÓN DE LA SESIÓN 5:
“Ubicamos los puntos de acumulación o quemado de basura”
2.2. 1.2.- PROPOSITO DE LA SESION 5:
Al finalizar la
sesión, el estudiante REPRESENTA la distancia entre dos puntos desde su forma
algebraica.
2.2. 1.3.- SITUACION SIGNIFICATIVA.
“Los vecinos de un sector del
distrito de Monsefú, han detectado gran acumulación de basura por parte de
algunos vecinos y otros no. La acumulación de basura es en distintos puntos de
la cuidad, específicamente en los entre las calles Bolognesi y Sucre (A) y José
Quiñones y Sucre (B); por ello, que establecer un plan para evitar está
problemática. Para ellos se pregunta ¿Cómo se podrá hallar la distancia entre
estos puntos señalados? ¿En qué no beneficiará saber la distancia entre estos
dos puntos? ¿Y cómo podría representar matemáticamente?
Ante este hecho, como estudiantes
de la I.E San Carlos, identificados con la problemática de nuestro distrito: ¿Qué acciones podrían tomar para brindarle nuestra ayuda?,
¿De qué manera?
SEGUNDA
PARTE: LECTURAS
2.12.1.- PLANO CARTESIANO
El plano cartesiano es utilizado como un
sistema para localizar y representar puntos en el plano. A partir de la
ubicación de las coordenadas de dos puntos, surge la pregunta: ¿qué tan
apartados se encuentran los puntos? O formulada de otra manera: ¿cuál es la
distancia que hay entre ambos puntos?
Responder esta pregunta permite medir
distancias, que es una operación importante, ya que la medición permite reunir
información sobre diferentes procesos o fenómenos, para su estudio y
comprensión.
En esta lección, se presenta la fórmula para
calcular la distancia entre dos puntos, así como el proceso necesario para
deducirla a partir de conocimientos más básicos.
2.2. 2.2.- DISTANCIA ENTRE DOS PUNTOS
Ø La
distancia entre dos puntos en la recta numérica
Para calcular la distancia en la recta numérica
utilizamos el valor absoluto, y esta se calcula por la diferencia en la
posición de cada punto.
En los puntos ubicados en la recta numérica 2 y 6. ¿Cuál será su
distancia?
Ø La distancia entre dos puntos en el plano cartesiano:
Para calcular la distancia en el plano cartesiano
el procedimiento es distinto, se requiere del uso del teorema de Pitágoras
llamado así en honor al filósofo y matemático Pitágoras de Samos (569-475 a.C).
Este teorema se aplica a los triángulos rectángulos y relaciona las longitudes
entre los catetos y la hipotenusa. Esta
relación dice que, para todo triángulo rectángulo, el lado mayor (hipotenusa)
al cuadrado es igual a la suma de los cuadrados de los lados que conforman el
ángulo recto (catetos).
Se denomina distancia entre
los puntos y de un mismo plano, a la longitud
de un segmento de la recta que tiene como extremos A y B, se representa “d”,
donde “d” es distancia entre A y Q.
TERCERA PARTE:
3.1 VIDEOS DE REFUERZOS: Ingresar a los siguientes links y analizar:
Ø
Distancia
entre dos puntos
https://www.youtube.com/watch?v=dRv6f7Y2l6U
Ø Distancia entre dos puntos en el plano
cartesiano ejercicios resueltos método gráfico.
https://www.youtube.com/watch?v=OsvggSiRWrU
1)
¿Cuál es
la distancia entre los puntos (-1, -3) y (5, 7)? Representa la distancia en plano cartesiano.
a)
11.66 b) 12.64 c) 13,44 d) 13 e) N.A
2)
Hallar la
distancia entre los puntos A (2, −5) y B (−4, −1). Representar en el plano
cartesiano.
a) 7.2 b) 6.8 c) 4.8 d) 5 e) N.A
3)
Si la
distancia de A (2; 2) a B (5; b) es 5 y la distancia de este último a C (c; 3)
es
.sabiendo que (b > 0 y c ≠ 0). Hallar los valores de b y c.
Representar los puntos en plano cartesiano.
a) 2 y 10 b) 3 y 10 c) 4 y 2 d) 7 y 11 e) N.A
Actividad 2: PROBLEMAS
P1: Los vecinos de Monsefú, se han propuesto colocar tachos de basura para evitar el acumulo de basura. Sabiendo que la casa de marcos está 10 metros hacia la derecha y 5 hacia el norte donde vive Luis. ¿Qué distancia deberá de caminar sabiendo que los tachos de basura se encuentran a metros 20 la derecha y 10 metros al norte de su casa?
a) 20.40 b) 30.25 c) 22.35 d) 35 e) N.A
P2: En una reunión municipal, se estableció colocar tachos de basuras procurando las tres RRR. Si se llegó al cuerdo que se pondrá tres recipientes de basura para plástico, residuo y vidrío, cada 8 m en la trayectoria de los puntos de acumulación de basura de A (-3, -2) y B (5,8). ¿Qué distancia hay desde de A hacia B? ¿Y cuántos recipientes de basura en total se colocaron de A hasta B, si parten desde el punto A?
a) 12,80 m y 6 b) 11,80 m y 3 c) 12,80 m y 3 d) 12 m y 9 e) N.A
P3: Ciertos estudiantes empiezan a investigar lugares que concienticen a la población sobre el no votar basura, inician desde la casa Luis que está ubicado en (-5,-2) y luego caminan a la derecha hasta una gruta que está en (3,-2). Luego siguen hacia el norte hasta un pozo que está en (3;4) y, finalmente, caminan con dirección sur- este hasta el punto (7,2) donde encontrón carteles concientizando a las personas de no votar la basura. ¿Cuál será la distancia total recorrida por cada uno de los estudiantes hasta haber encontrado los carteles que concientizan a las personas? Representa la distancia recorrida en plano cartesiano.
a) 16 b) 18,47 c) 15 d) 20,54 e) N.A
QUINTA PARTE
Después de haber realizado tu trabajo, reflexiona con tus compañeros respondiendo las siguientes preguntas.
¿Para qué nos son útiles determinar la distancia entre dos puntos? ¿Para qué lo aprendiste?
¿Qué dificultades encontraste y que hiciste para superarlas? ¿Podrías comentar en qué otras situaciones podemos utilizar dichos conocimientos? ¿por qué crees que algunos tienen una respuesta diferente?, ¿qué nociones relacionaste?, ¿cuáles fueron las que más encontraste?
SEXTA PARTE
6.1 RETO: Completar los cuestionarios propuestos resolviendo las preguntas, dada por el docente en aula de acuerdo a la sesión desarrollada.
6.2 ENTREGA: En físico, de manera presencial.
¡BUENA SUERTE ¡
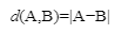
No hay comentarios:
Publicar un comentario