“Año del Bicentenario del Perú: 200 años de independencia”
MATERIAL DE LECTURA-S4-P2-2021-MAT.3º
PRIMERA
PARTE: LECTURAS
I.- PERIMETRO, AREA Y VOLUMEN.
1.1.-
¿Qué es el perímetro de una figura geométrica?
El perímetro de una figura
geométrica plana, es igual a la suma de las longitudes de sus lados
o contorno. El perímetro es, por tanto, una medida de longitud, por
lo que vendrá en centímetros, metros, pulgadas, etc. En general, en unidades
lineales.
NOTA: Para hallar el perímetro de una
figura sólida (tridimensional),
depende de las figuras planas (bidimensional)
que lo formen.
1.2.- ¿Qué es el área de una
figura geométrica?
El Área de una Figura Geométrica, es el
espacio que queda encerrado entre los límites de una figura; es decir, nos da una idea de qué tanta superficie cubre dicha
figura. Para calcular el área de algunas de las figuras geométricas,
utilizamos una serie de fórmulas.
1.3.-
¿Qué es el volumen de una figura geométrica?
El volumen
es una magnitud métrica de tipo escalar definida como la extensión en tres
dimensiones de una región del espacio. Es una magnitud, derivada de la
longitud; es decir, el volumen corresponde
al espacio que la forma ocupa, por lo tanto, es la multiplicación de la altura
por el ancho y por el largo. El volumen sirve,
por ejemplo, cuando queremos calcular la cantidad de agua en una piscina.
II.- FIGURAS TRIDIMENSIONALES
2.1-
DEFINICION: Las Figuras Tridimensionales son
también llamados sólidos. Son una porción del espacio limitado por caras planas
o curvas. A diferencia de las figuras geométricas comunes, que
solo tienen 2 dimensiones (Ancho, Largo),
estas tienen 3 dimensiones adicionándole la PROFUNDIDAD, es decir tienen: largo, ancho, profundidad (altura). Es
decir, cada uno de sus puntos puede ser localizado especificando tres números
dentro de un cierto rango. Aunque una superficie plana tiene dos
dimensiones, a partir de ellas podemos construir objetos tridimensionales.
2.2-
CARACTERISTICAS: Se considera atributo
medible a toda característica de un cuerpo que puede
ser cuantificado, como la longitud, la superficie y el
volumen. Ejemplo: anchura, altura y profundidad.
III.- FIGURAS GEOMÉTRICAS SÓLIDAS O CUERPOS GEOMÉTRICOS.
También se les conoce como formas o cuerpos
geométricos. Estas figuras tienen tres dimensiones (longitud, profundidad y altura), es
decir, son figuras que tienen volumen. Por ello, podemos
decir que ocupan un lugar en el espacio.
3.1.1.- POLIEDROS: La palabra poliedro proviene del
griego “polys” que significa muchas y de “edra” que
significa base o caras.
Estamos hablando entonces de formas geométricas que poseen varias caras y que
además son planas. En la vida real podemos encontrar un montón de objetos que
tienen forma de poliedros, como un cubito de hielo, una pirámide o un envase de
leche.
Entre ellos tenemos:
A.- POLIEDROS REGULARES: son también conocidos como sólidos platónicos y se
caracterizan por tener todas sus caras iguales. Un ortoedro es
un prisma rectangular ortogonal, cuyas caras forman entre sí ángulos diedros
rectos. A estos prismas rectos, y se los denomina paralelepípedos
Son cinco: tetraedro, cubo o hexaedro,
octaedro, dodecaedro e icosaedro.
PROBLEMAS RESUELTOS:
1.- Tengo una caja de
forma cuadrada, cuyo lado mide 8cm ¿Cuál es su perímetro, área
y volumen?
Solución: Aplicamos
características del cubo.
1º.- PERIMETRO: P = 12 . a
= 12 . 8
= 96 m
2º.- AREA:_A = 6.a2 = 6(8)2
= 6 (8 . 8) = 6 (64) = 384 cm 2
3º.- VOLUMEN: V = a3 = 83 = 8 . 8 . 8 = 512 cm3
Resp. P = 96m
; A = 384 cm2 y V
= 512 cm3
2.- Un ataúd de
medidas: largo 1,90cm, ancho: 0,60cm y altura: 0,5 cm ¿Cuál
es su área y volumen?
Solución: Aplicamos
características del paralelepípedo.
1º.- PERIMETRO: P = 4L + 4a + 4h = 4(1,90) + 4(0,60) + 4(0,5) = 7,60 + 2,40 + 2 = 12m
2º.- AREA:_A = 2(1,90 . 0,60 + 1,90 .
0,50 + 0,6 . 0,50) = 2(1,14 + 0,95 + 0,30) = 2 (2,39) = 4,78 cm 2
3º.- VOLUMEN: V = 1,90 . 0,60 . 0,50 = 0,57 cm3
Resp. P = 12cm
; A = 4,78 cm2 y V
= 0,57 cm3
C.- PIRÁMIDES: ESTÁN COMPUESTAS POR UNA CARA POLIGONAL (CUADRADOS, TRIÁNGULOS, ETC) QUE ES SU BASE Y POR CARAS LATERALES (LADOS) CON
FORMA DE TRIÁNGULOS.
1.- Juan es un niño
que, por su cumpleaños, le han reglado un frugus de forma triangular, que tiene
una base cuadrada, cuyo lado mide 4 cm, una altura de 12 cm y de 16cm de
apotema ¿Cuál es su perímetro, área y volumen?
Solución: Aplicamos
características de la pirámide.
1º.- PERIMETRO: P = 4.Ap + 4a
= 4.16
+ 4.4
= 64cm + 16cm
= 80cm
2º.- A = 4 (2 . 16 + 4) = 4 (32 + 4) = 4 (36)
= 144 cm 2
3º.- V = 1/3 . 42 . 12 =
Resp. P = 80cm
; A = 144 cm2 y
V
= 48 cm3
2.- El hermano de
Juan, para molestarlo ha comprado un frugus de base pentagonal, cuyo lado mide
7 cm, la altura de pirámide 14 cm, la altura de una cara es 16 cm y 3 cm de apotema ¿Cuál
es su perímetro, área y volumen?
Solución: Aplicamos
características de la pirámide. Base un pentágono que tiene 5 lados y costado 5
triángulos.
1º.- PERIMETRO: P = 5.Ap + 5a
= 5.3
+ 5.7
= 15cm + 35cm
= 50cm
2º.- LUEGO PARA
HALLAR EL AREA:
Hallando 1º el área
lateral. Donde: Pb = perímetro de la base; Hc =altura de una de las caras.
3º.- HALLAMOS SU
VOLUMEN:
V =
RESPUESTAS: P = 50cm ; A = 332,50 cm2 ;
V = 245
cm3
3.1.2.- CARACTERÍSTICAS
DE LOS POLIEDROS:
a.- Caras: las caras de los poliedros son las superficies planas
que limitan al poliedro.
b.- Aristas: las aristas de los poliedros son los lados que
conforman cada cara.
c.-
Vértices: los vértices de los poliedros son los
puntos donde se interceptan las aristas. Tres caras se unen en un mismo
vértice.
IV.- CUERPOS REDONDOS.
Son aquellas figuras geométricas sólidas, compuestas por
superficies curvas en su totalidad o por superficies planas y curvas. La forma
de los cuerpos redondos la podemos encontrar en muchos elementos de la vida
real, como en la forma de un volcán (cono), de una bola de billar (esfera) o en
un bote de pintura (cilindro).
¿Qué es el diámetro? En geometría,
el diámetro es el segmento de recta que pasa por el centro y une dos
puntos opuestos de una circunferencia. Formado por dos RADIOS (D = r + r)
Entre los cuerpos redondos más
comunes encontramos:
4.1.- CONO: se trata de un cuerpo redondo compuesto por una base
circular y una superficie curva.
Elementos de un cono, su área y volumen.
4.4.- LA SEMIESFERA: es la mitad de una esfera:
PROBLEMAS RESUELTOS:
PROBLEMA 1.- Un alumno ha
recibido un gorrito de cumpleaños forma de cono), cuyas medidas son: su radio
mide 7cm, su altura 28 cm, su generatriz mide 29 cm. Si π = 3,14 ¿Cuál
es su área y volumen?
Solución:
Aplicamos las características del CONO.
Solución: Aplicamos
características de la pirámide.
1º.- PERIMETRO:
a) Del circulo: L = 2πR
b) Del semicírculo:
Tenemos: L = 43,93/ 4 = 10,99cm
TOTAL: Circulo + Semicírculo = 43,93cm +
10,99cm = 54,92cm
2º.- PARA EL AREA: Hallamos
primero, el área lateral, luego el área total.
AL = 3,14 . 7 . 29 = 637,42 cm2
AT = 637,42 + (3,14 . 72) = 637,42 + 153,86 = 791,28 cm2
3º.- PARA EL VOLUMEN:
V =
RESP.
P
= 54,92cm ; A = 791,28cm2 y
V
= 1436,03 cm3
PROBLEMA 2.- Tengo un balón
cuyo radio mide 15 cm. Si π = 3,14 ¿Cuál es su perímetro, área
y volumen?
Solución:
Aplicamos las características de la ESPERA.
1º.- PERIMETRO: L = 2π
2º.- PARA SU AREA:
Hallamos primero, el
área.
A = 4 . 3,14 . (15cm)2 = 12,56 . 225 = 2826 cm2
3º.- Hallamos el
VOLUMEN:
V =
ESP. P = 94,20 cm ; A = 2826 cm2 y V = 14 130 cm3
Solución:
Aplicamos las características del CILINDRO.
1º.- PERIMETRO: L = 2π
2º.- PARA AREA:
Hallamos primero, el
área lateral.
AL = (2 . 3,14 . 0,45) 1,40 = (2,83) 1,40 = 3,96 m2
HALLAMOS EL AREA DE LA BASE.
Ab = 3,14 (0,45)2 = 3,14(0,20) = 0,64 m2
HALLAMOS EL AREA TOTAL.
AT = 3,96
+ 2 (0,64) = 3,96 + 1,28 = 5,24 m2
V = 0,64 . 1,40 = 0,896 m3
RESP.
P
= 2,83 cm ; A = 5,24 cm2 y
V
= 0,90 cm3 (redondeado)
Visualizar los siguientes videos:
1.- https://www.youtube.com/watch?v=jogZRNrihac&ab_channel=DanielCarre%C3%B3n
Diferencia entre perímetro, área y volumen
2.- https://www.youtube.com/watch?v=Xlz3EdHxFvY
perímetro, área y volumen de figuras sólidas
(01).
3.- https://www.youtube.com/watch?v=i0bHMCIiRbU&ab_channel=JoseAntonioMulaMarcoJoseAntonioMulaMarco
perímetro, área y volumen de figuras sólidas (02).
TERCERA PARTE:
3.1.- SOBRE LA LECTURA: Responder a las siguientes preguntas:
3.1.1.-
¿Qué es el perímetro, área y volumen de una figura geométrica?
3.1.2.-
¿Qué son figuras tridimensionales?
3.1.3.-
¿Cuáles son las figuras geométricas sólidas o cuerpos geométricos?
3.1.4.-
¿Un paralelepípedo de cuantas figuras bidimensionales está formada?
3.1.5.-
¿Un cilindro de cuantas figuras bidimensionales está formada?
3.1.6.-
¿Una pirámide de base pentagonal, de cuantas figuras bidimensionales está
formada?
3.2.- SOBRE LOS VIDEOS: Responder a las siguientes
preguntas:
3.2.1.-
¿Cuál es el nombre del video 1º? Explica el ¿por qué?
3.2.2.-
¿Cuál es el nombre del video 2º? Explica el ¿Por qué?
3.2.3.-
¿Cuál es el nombre del video 3º? Explica el ¿Por qué?
3.3.- APLICA LO APRENDIDO:
Resolver los
ejercicios de las paginas 159 al 170 del Cuaderno de trabajo de Matemática. Si no lo tienes,
ubicarlo en el siguiente link:
https://drive.google.com/file/d/1aITECLVLQcq1BnShJPmD0J8KeHgKdDWH/view
CUARTA PARTE:
RETO: Presenta el siguiente producto:
1.- Halla el perímetro, el área y volumen de la figuras que has
considerado como instrumento para moler los alimentos en la sesión 3.
2.- Toma una foto a tu trabajo y lo envías a tu profesor.
QUINTA PARTE:
VISITAR
el Blog:
https://saelmatematico.blogspot.com/
En este blog, encontraras lo necesario para prepararte para la sesión
correspondiente o de lo contrario brinda tus comentarios, referentes a lo leído
y visualizado y sobre lo que podrías necesitar para tu mejor aprendizaje.
......................................................
Vallejos MARRUFO, Elías.
PROFESOR
“Educar
es más que dar carrera para vivir, es templar el alma para las dificultades y
para soportar las injusticias” –PITÁGORAS







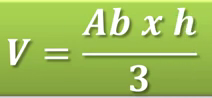















No hay comentarios:
Publicar un comentario