SESION 6-P2-MAT.3º

 

“Año del Bicentenario del Perú: 200 años de independencia” 

MATERIAL DE LECTURA-S6-P2-2021-MAT.3º

PRIMERA PARTE:

I.- PROPOSITO DELA SESION:

 “Usamos fracciones y decimales para comprar cantidades de alimentos molidos, para preparar platos típicos”.

 SEGUNDA PARTE: LECTURAS

1.- LOS NUMEROS RACIONALES.

Los números racionales, son todos los números que pueden representarse como: FRACCIONES (el cociente de 2 números enteros (z) es decir una fracción común,{\displaystyle a/b} parte de un todo, con numerador {\displaystyle a}  y denominador {\displaystyle b}  distinto de cero) y  DECIMALES (finito o semiperiodico).

 El conjunto de los números racionales se denota por “Q” y es un subconjunto de los números reales ({\displaystyle \mathbb {R} }R), es decir: Q ⊂ R.

 

2.- RELACIONES DE EQUIVALENCIA Y ORDEN CON FRACCIONES.

2.1.- INMERSIÓN DE ENTEROS: Cualquier entero “n” se puede expresar como el número racional n/1 debido a eso se escribe frecuentemente {\displaystyle \scriptstyle \mathbb {Z} \subset \mathbb {Q} }: Z ⊂ Q

2.2.- LEY DE EQUIVALENCIA: Si se cumple:

 

 Ejemplo 1: ¿Son iguales o no 1/4 y 2/5?

Decimos que NO, porque: 1 x 5 = 5   y  4 x 2 = 8

ENTONCES: 1/4  ≠   2/5

Ejemplo 2: ¿Son iguales o no 1/4 y 3/12?

Decimos que SI, porque: 1 x 12 = 12   y  4 x 3 = 12

ENTONCES: 1/4  = 3/12

 2.3.- ORDEN:

 Ejemplo 1: ¿Cuál es la relación de orden entre 1/4 y 2/5?

Decimos que: 1/4  “es menor que”   2/5, porque: 1 x 5 = 5   y  4 x 2 = 8

ENTONCES: 1/4  <   2/5

Ejemplo 2: ¿Ordenar de menor a mayor: 1/2, 1/4, 1/3 , 1/5?

SOLUCION:

Vemos la equivalencia de dos en dos y vamos descartando. Quedando:

1/5  < 1/4  < 1/3 < 1/2

 3.- NÚMERO RACIONAL EN BASE DECIMAL.

Todo decimal nace de una fracción, al dividir el NUMERADOR entre el DENOMINADOR:

Ejemplo: 1/2 = 0,5

3.1.- TIPOS: Los decimales pueden ser de tres tipos:

3.1.1.- EXACTA: la parte decimal tiene un número finito de cifras. Al no ser significativos, los ceros a la derecha del separador decimal pueden omitirse, lo que da por resultado una expresión «finita» o «terminal».

Ejemplo: 8/5 = 1,6    ; 1/2 = 0,5  , etc.

3.1.2.- {\displaystyle {\frac {8}{5}}=1,6}PERIÓDICA PURA: toda la parte decimal se repite indefinidamente.

Ejemplo: 1/3 = 0,333333333333333……        {\displaystyle {\begin{array}{rcl}{\cfrac {1}{7}}&=&0,142857142857\dots \\&=&0,{\overline {142857}}\end{array}}}

3.1.3.- PERIÓDICA MIXTA: no toda la parte decimal se repite.

Ejemplo: 1/6 = 0,166666666……..

 

3.2. TABLERO DE VALOR POSICIONAL DE LOS DECIMALES.

 

 Ejemplo 1:           0,4 se lee: “cuatro décimas”

Ejemplo 2:           1,03 se lee: “un entero tres centésimos”.

Ejemplo 3:           0,0023 Se lee “veintitrés diez milésimos”.

 

3.3.- RELACIONES DE ORDEN ENTRE NÚMEROS DECIMALES.

3.3.1.- Para comparar números decimales, puedes comparar las partes enteras de los números decimales entre sí y luego las cifras decimales según su posición, comenzando por la de mayor valor (décimos), hasta que una de ellas sea de menor  o mayor que la otra.

Ejemplo: comparar 4,25 y 4,21

SOLUCION:

Comparamos cada cifra decimal, teniendo en cuenta el tablero de V.P

 Por lo tanto:  4,25 > 4,21

3.2.2.- Cuando tenemos números decimales, con distintas cantidades de cifras decimales después de la coma. Para comparar si un número decimal es mayor, menor o igual a otro podemos igualar con ceros las cifra decimales para que cada cantidad tenga el mismo número de cifras decimales después de la coma.

Ya igualadas las cifras procedemos a comparar y a ubicar en la posición que le corresponde.

Ejemplo: Cuál número es mayor entre 0,2 y 0,85.

SOLUCION

  Por lo tanto: 0,2 < 0,85

                                                               

TERCERA PARTE:

Visualizar los siguientes videos:

3.1.- https://www.youtube.com/watch?v=c9eWZ5zlzP0&ab_channel=P%C3%ADldorasmatem%C3%A1ticasP%C3%ADldorasmatem%C3%A1ticas

3.2.- https://www.youtube.com/watch?v=qczf0hsvvV0&ab_channel=Profa.KempisProfa.Kempis

 

3.3.- https://www.youtube.com/watch?v=bW4qeHL2Gk8&ab_channel=MaribelEspinozaUnPocodeTodo%28UnPocodeTodo%29

 

CUARTA PARTE: QUESTIONARIOS

4.1.- SOBRE LA LECTURA: Responder a las siguientes preguntas:

4.1.1.- ¿Qué son los números racionales?

4.1.2.- ¿Cuáles son los sub-conjuntos que la conforman?

4.1.3.- ¿Cuál es la ley de equivalencia?

4.1.4.- ¿Cuáles son los 5 primeros órdenes, del tablero de valor posicional de los decimales?

4.2.- SOBRE LOS VIDEOS: Responder a las siguientes preguntas:

4.2.1.- ¿Cuál es el nombre del video 1º? Explica el ¿por qué?

4.2.2.- ¿Cuál es el nombre del video 2º? Explica el ¿Por qué?

4.2.3.- ¿Cuál es el nombre del video 3º? Explica el ¿Por qué?

4.3.- RESOLVER:

4.3.1.- EJERCICIOS CON FRACCIONES:

1º) ESCRIBE EN CADA CASILLERO EL SIMBOLO > ; <   Ó  = SEGÚN CORRESPONDA:

 

2º) ESCRIBE EN CADA CASILLERO LA FRACCION QUE CORREPSONDA SEGÚN SU ORDEN:

 

 

3º) RESOLVER FICHA DE TRABAJO ADJUNTA (fracciones gordas y flacas).

 

4.3.2.- EJERCICIOS CON DECIMALES:

1º) ESCRIBE EN CADA CASILLERO EL SIMBOLO > ; <   ó =  SEGÚN CORRESPONDA:

 

 3º) RESOLVER FICHA DE TRABAJO ADJUNTA (fracciones gordas y flacas).

 4.3.2.- EJERCICIOS CON DECIMALES:

 

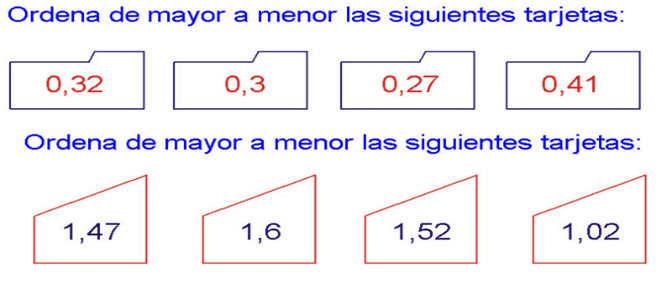
 2º) ORDENAR:

3º) Escribe dentro de cada paréntesis “V” si la afirmación es correcta y “F” si es falsa.

 

4.3.3.- PROBLEMA:

A los alumnos de un grupo de 3º de Secundaria de la I.E “San Carlos”, se les solicitó sus respectivos pesos. Los únicos que lo sabían, lo registraron de la siguiente manera: DANIEL 20,40kg, ALICIA veinte kilos con treinta gramos, FERNANDO 20¼ kg, MAURICIO 20,50 kg, PEDRO veinte y medio, SOFÍA 20 1/5 kg y TERESA dijo que tenía más o menos un peso de veinte mil cuatrocientos ochenta gramos.

1. ¿Quién es el que pesa menos?

2. ¿Hay alumnos que pesan lo mismo? ¿Quiénes?

3. Al compararse TERESA con sus compañeros, se da cuenta de que pesa más que DANIEL y más que Pedro. ¿Cuánto crees que pesa?

NOTA: Anotemos las cantidades del problema en una tabla.

 

4.3.4.- APLICA LO APRENDIDO:

Resolver los ejercicios de la página 98 del Cuaderno de trabajo de Matemática. Si no lo tienes, ubicarlo en el siguiente link:

https://drive.google.com/file/d/1aITECLVLQcq1BnShJPmD0J8KeHgKdDWH/view

 

QUINTA PARTE:

RETO: Presenta el siguiente producto:

1.- EXPRESAR números decimales y fraccionarias en un cuadro de doble entrada, al comparar la cantidad de alimentos molidos para preparar platos típicos. (Usar datos del producto de la sesión 4)

2.- Toma una foto a tu trabajo y lo envías a tu profesor.

SEXTA PARTE:

VISITAR el Blog: https://saelmatematico.blogspot.com/

En este blog, encontraras lo necesario para prepararte para la sesión correspondiente o de lo contrario brinda tus comentarios, referentes a lo leído y visualizado y sobre lo que podrías necesitar para tu mejor aprendizaje.

......................................................

Vallejos MARRUFO, Elías.

PROFESOR

 

 

 

 

 

 

 

 

 

“Educar es más que dar carrera para vivir, es templar el alma para las dificultades y para soportar las injusticias” –PITÁGORAS