ANEXO 1
“Año del Bicentenario del Perú: 200 años de independencia”
MATERIAL DE LECTURA PARA LA SESION Nº5-P4.MAT.3º
PRIMERA PARTE:
1.1.- DENOMINACION DEL PROYECTO BIMESTRAL-P4:
"Desde
la matemática desarrollamos EMPRENDIMIENTO en familia y comunidad para
fortalecer la economía en nuestro hogar, con actividades auténticas".
1.2.- DENOMINACION DEL PROYECTO DE GRADO:
"Producción y venta de yogurt, vinagre, vino y
encurtidos".
1.3.- DENOMINACION DE LA SESION 5:
“Descubrimos
la regla de formación de una P.G”
SEGUNDA PARTE:
2.1.- PROPOSITO DE LA SESION:
EXPRESAR la
reglas de formación en una progresión geométrica.
2.2.- SITUACION SIGNIFICATIVA:
MARYORI estudiante de la institución educativa “San Carlos” de Monsefú,
ha puesto a la venta una serie de productos, de su negocio emprendedor; pero,
no puede determinar la cantidad exacta de venta, en un día y mes determinado ¿Cómo podemos ayudarla? ¿Qué nociones debe
adquirir?
TERCERA PARTE: “LECTURAS”
Una sucesión es un
conjunto ordenado de números u objetos, llamados términos. Cada término de la
sucesión se representa con una letra minúscula con subíndice. a1, a2,
a3, a4, a5, a6, etc. (Se lee: a sub.1, a
sub.2, etc).
EJEMPLO:
► En la sucesión 2, 7, 12, 17, 22,
…
a1
= 2 indica que el primer término de la sucesión es el 2
a2 = 7 indica que el
segundo término de la sucesión es 7
a3 = 12 indica que el
tercer término es el 12
a4 = 17 es el cuarto
término, etc.
3.2.1.- TIPOS: Una sucesión es finita
cuando tiene primer y último término. Una sucesión es INFINITA
si tiene primer término, pero no tiene último término.
Ejemplo
► La sucesión 5, 10, 15, 20, 25 es finita.
Su primer término es a1 = 5 y el último a5 = 25.
► La sucesión 2, 7, 12, 17, 22, ….…
Es infinita. Su primer término es
a1 = 2 y no tiene
último.
3.2.2.- TERMINOS DE UNA SECESION: Los términos de
algunas sucesiones, se pueden determinar siguiendo un criterio, que se denomina
“REGLA DE FORMACIÓN”, que relaciona
cada término con el lugar que ocupa.
EJEMPLO: Las dos reglas
fundamentales son:
► Sumar
una misma cantidad. En la sucesión: 2, 7, 12, 17, 22, 27 …
cada término es el anterior más 5.
► Multiplicar
por una misma cantidad. En la sucesión: 3, 9, 27, 81, 243, 729…
cada término es el anterior por 3.
En una sucesión, el término que
ocupa una posición cualquiera, “n”, se llama TÉRMINO GENERAL y se
escribe an.
EJEMPLO: La sucesión 2, 4,
6, 8, 10, … es la formada por los números pares.
El término general de esta sucesión
es an = 2 · n.
Tenemos:
a1 = 2 · 1 = 2
a2 = 2 · 2 = 4
a3 = 2 · 3 = 6,
…
an = 2 · n
3.2.-
PROGRESIONES GEOMÉTICAS.
3.2.1.- DEFINICION: Una progresión
geométrica, es una SUCESIÓN en la que cada término, salvo el primero, se
obtiene multiplicando el anterior por una cantidad fija “r”, llamada RAZÓN
de la progresión.
Ejemplo
► 5, 15, 45, 135,
405, … es una progresión geométrica de razón 3. Cada término se obtiene
multiplicando el anterior por 3. a1 = 5, a2 = 5 · 3 = 15, a3 = 15 · 3 = 45, …
3.2.2.- TERMINOS: El término
general de una progresión geométrica es:
an
= a1 · r n-1
Donde a1 es el primer
término, y r, la razón.
Ejemplo
► Si se conoce el
primer término a1 = 5 y la razón es r = 3, entonces podemos
conocer el término general de esa sucesión: an = 5
· 3 n – 1
Y cualquier valor
concreto de la sucesión, por ejemplo, el término a5 es:
a5 = 5 · 3 5 – 1
= 5 · 3 4 = 5 · 81 = 405
3.2.3.- SUMA DE
UNA PROGRESION GEOMETRICA.
En una progresión
geométrica, la suma de los n primeros términos es: Sn = a1 · a2 + a3 + … + an-1
+ an =
S = (an.r – a1) / r – 1 ó S = (a1.rn - a1)/r-1
EJEMPLO 1:
► En la progresión geométrica 5,
15, 45, 135 la suma de términos es:
SOLUCION
Donde: a1 =
5 ; an = 135
La razón es: 3; porque: 3.5 =
15 ; 15.3 = 45; etc.
Como tenemos ultimo termino, usamos
la primera formula.
Reemplazamos:
S = (an.r – a1) / r – 1 = (135 . 3 - 5)/ 3 –
1 = 400/2 = 200
EJEMPLO 2:
En
una progresión geométrica el primer término vale 1, el segundo 3. …….La suma de
todos los términos 29524 ¿Cuántos términos tiene?
SOLUCIÓN
Formamos la PG: 1, 3, 9, …..
Como
no tenemos la ultimo termino, usamos la segunda formula:
Donde:
a1=
1
r =
3
(a1.rn - a1)/r-1
= (1 . 3n - 1)/3-1 =
29524 = 3n
- 1/2
59048 = 3n
- 1
59049 = 3n
310 = 3n
Como los coeficientes
son iguales, entonces los exponentes serán iguales.
Luego: n = 10
3.3.-
PROBLEMAS RESUELTOS.
P1.-
Calcular la RAZÓN de la progresión: 1,
2, 4, 8, 16, ……...
SOLUCION
En una Progresión geométrica, la RAZON suele denotarse por “r” y se calcula dividiendo un término entre el término
anterior:
Entonces tenemos:
Por lo tanto, la RAZON
es 2.
P2.- Calcular el TERCER y SEXTO término de la sucesión de la
progresión: 1,
2, 4, 8, 16, ……...
SOLUCION
El término general de la progresión de los ejemplos anteriores es:
Por lo tanto:
P3.- Calcular la suma de los 8 primeros términos de la progresión
de las potencias de 2:
SOLUCION
Podemos calcular la suma de los primeros “n” términos de una progresión geométrica mediante la fórmula:
Luego:
Si “n” = 8 y r = 2 , reemplazamos en formula:
P4.- La progresión:12; 6; 3; 1,5; 0,75; ……..
la SUMA de todos sus términos es.
SOLUCION
Si una progresión geométrica tiene una razón “r” entre −1 y 1 (es decir, |r| <1 ), podemos sumar todos los
términos de la progresión infinita mediante la fórmula: S ꝏ = a1 / 1 - r
Entonces reemplazando.
S ꝏ
= a1 / 1 - r = 12/1 – 0,5 = 12/ 0,5 = 24
P5.- Calcular la suma de los primeros 5 términos de la progresión geométrica con
razón r = 0,5 y
cuyo primero término es a1 = 16.
SOLUCION
Usamos la fórmula para sumar los primeros términos:
S5 = 16 [(0,55 – 1)/
0,5 – 1) ]
S5 = 16 [(0,03125 – 1)/ -0,5
]
S5 = 16 [-0,96875/ -0,5 ]
S5 = 16 [1,9375]
S5 = 31
P6.- El tercer término de una progresión
geométrica es a3 = −25 y la razón
es r = −5. ¿Cuál es el primer
término?
SOLUCION
El término general es: an
= a1 · r n-1
Reemplazando datos:
an
= a1 · r n-1
a3 = a1 · (-5) 3-1
-25 = a1 · (-5) 2
-25 = a1 · 25
a1 = -25/25
a1 = -1
P7.- El quinto y el sexto término de una
progresión geométrica son a5 = 80 y a6 = 160. ¿Cuál es el primer
término?
SOLUCION
Como los términos son consecutivos, podemos calcular la razón fácilmente:
La fórmula del término general es:
Como conocemos r = 2 y a5 = 80 , podemos calcular a1:
a5 = a1 · (2) 5-1
80 = a1 · (2) 4
80 = a1 · (16)
a1 = 80
/16
a1 = 5
P8.- El lunes Jaime cuenta un secreto
a 5 amigos. Al día siguiente, estos 5 amigos cuentan el secreto a otros 5 amigos. Al día siguiente, las nuevas personas que
saben el secreto también lo cuentan a otras 5 personas. Y, así,
sucesivamente.
Suponiendo que cada persona sólo ha
contado el secreto a otras 5, ¿cuántas personas
saben el secreto el domingo?
SOLUCION
Construimos una sucesión: el término “an” es el número de
personas que descubren el secreto en el día número “n”.
El primer día sólo Jaime conoce el secreto: a1 = 1
El segundo día, Jaime cuenta el secreto a 5 amigos: a2 = 5
El tercer día, cada uno de los 5 amigos cuenta el secreto a otros 5, así que el número de personas que se enteran es: a3 = 5 . 5 = 25
Y así, sucesivamente.
Se trata de una progresión geométrica con
razón r = 5.
El número de personas que saben el secreto el
domingo es S7. Lo calculamos usando:
Sn = a1 [(rn – 1)/ r – 1) ] =
S7 = 1 [(57 – 1)/ 5 –
1) ]
S7 = 1 [(78124 – 1)/ 4 ]
S7 = 1 [78123/ 4]
S7 = 1 [19 531]
S7 = 19 531
P9.- Una sucesión geométrica con
primer término a1 = 2 tiene
razón r = 0,3. ¿Cuál es la suma de los 6 primeros términos? ¿Y la suma de todos sus
términos?
Sol SOLUCION
Calculamos la suma de los 6 primeros términos:
S6 = a1 [(rn – 1)/ r – 1) ] =
S6 = 2 [(0,3)6 – 1)/ 0,3
– 1) ]
S6 = 2 [(0,000729 – 1)/ -0,7]
S6 = 2 [-0,999271/ -0,7]
S6 = 2 [1,42753]
S6 = 2,86
Como la razón es |r| < 1, podemos sumar todos los
términos de la sucesión:
S ꝏ
= a1 / 1 - r = 2/1 – 0,3
S ꝏ
= 2/ 0,7
S ꝏ
= 20 : 7
S ꝏ
≡ 2,86
P.10.- La suma de los primeros 5 términos de una PG con razón r = −2 es S5=−77. ¿Cuál
es el primer término?
SOLUCION
La suma de los 5 primeros términos
es:
Como sabemos que S5=−77 y que r = −2,, reemplazamos:
-77 = a1 [(-2)5 – 1)/ -2 – 1) ]
-77 = a1 [(-32 – 1)/ – 3 ]
-77 = a1 [-33/ -3 ]
-77 = a1 . 11
a1 = -77:
11
a1 = -7
CUARTA
PARTE: VIDEOS DE REFURZO: Ingresar
a los siguientes links y analizar:
4.1.- LA SUCESION:
https://www.youtube.com/watch?v=FGoSqeFl5zg&ab_channel=DanielCarre%C3%B3n
4.2.- PROGRESION GEOMETRICA:
https://www.youtube.com/watch?v=q-c5VLWvL6w&ab_channel=SusiProfe
4.3.- TERMINO E-NESIMO:
https://www.youtube.com/watch?v=U-hhp4x4JcE&ab_channel=Matem%C3%A1ticasprofeAlex
5.1.- QUESTIONARIO:
1.- Es un conjunto ordenado de números, objetos o términos
Una
sucesión
Conjunto
Números
Conjunto
2.- Expresar cual es “a sub siete”
A7
a7
7ª
a7
3.- Indica
que “el tercer término es el 12”:
A
+12
12a
= 3
A3 = 12
an = 12 +3
4.- ¿Cuál es la razón en: 2, 8, 32, …….?
32
1
6
4
5.- El término general de
una progresión geométrica es:
an = a1 · r n-1
Sn
= (an.r – a1) / r – 1
Sn
= (a1.rn - a1)/r-1
r
= an+1/an
5.2.- PROBLEMAS PROPUESTOS SOBRE P.G:
P1.-
Un alumno al revisar sus cuentas, de su gran negocio emprendedor, encuentra que
el sexto y noveno día de la semana ha vendido en soles: a6 = 400 y a9 = 3600. ¿Cuánto vendió el primer día?
a) 0,07 b) 7,00 c) 0,007 d) 0,00007 e) NA
P2.- El lunes, Jaime es un gran vecino de Monsefú, cuenta que tú tienes una herniosa tienda que vende PRODUCTOS DE CALIDAD, a 10 amigos. Al día siguiente, estos 10 amigos lo cuentan a otros 10 amigos. Al día siguiente, las nuevas personas que lo saben, también lo cuentan a otras 10 personas. Y, así, sucesivamente.
Suponiendo que cada persona sólo ha contado de tu tienda a otras 10 ¿Cuántas personas saben de tu tienda el día domingo?
a) 1 111 111
b) 1 111 c) 11 111
d) 1, 111 e) NA
P.3.- Un alumno que se dedica a la venta de productos de limpieza, La
suma de los primeros 5 días de venta, si la razón de
vente de su primer día es la razón r = 5 es S5= 3 500 ¿Cuál es la venta del primer día?
a) 4,481 b) 44,80
c) 4481 d) 448,1 e)
NA
SEXTA PARTE:
6.1.- RETO: ELABORAR
un problema de venta de productos, según tu plan de negocio, aplicando la REGLA DE FORMACION de una P.G.
6.2.- ENVIO: Captura a través de WhatsApp.
......................................................
Vallejos MARRUFO, Elías.
PROFESOR
ANEXO 2
I.- “QUIZIZZ”: Control de lecturas y videos.
ANEXO 3
II.-
EJERCICIOS EN Whiteboard.fi: Ejercicios
del cuaderno de la parte quinta.
”Educar es más que dar carrera para
vivir, es templar el alma para las dificultades y para soportar las
injusticias” –PITÁGORAS










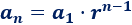







No hay comentarios:
Publicar un comentario