“Año del
Fortalecimiento de la soberanía nacional”
MATERIAL DE LECTURA-S5-P2-3°G-22
PRIMERA PARTE:
1.1.- DENOMINACION DE LA SESION 5:
1.2.- PROPOSITO DE LA SESION 5:
Al finalizar la
sesión 5, el estudiante ESTABLECERA relaciones entre dos
variables de un sistema de ecuaciones lineales, de acuerdo a una situación
significativa.
1.3.- SITUACION SIGNIFICATIVA.
MARIANA, se emocionó al ver tejer un paño, con el empleo de
tantos hilos y sobre todo, cuándo la señora artesana le contesto a su
inquietante pregunta: “Para hacer esta paño, estoy usando el color
rojo y el color amarillo, dando un total de ochocientas hilos; es decir, me
parece menos de lo que utilice en un paño anterior. Que use cuatro veces el
color rojo menos el doble de color amarillo, que me dio mil cuatrocientos hilos”.
MARIANA, tratando de entender
la información recibida, se pregunta: ¿Cómo representaría las cantidades de dichos colores?, ¿Cuántos
hilos de color rojo y amarillo son?, ¿Qué método de solución sería el más
adecuado?
SEGUNDA PARTE: LECTURAS.
2.1.- TENGAMOS EN CUENTA: Traducimos de lenguaje verbal a lenguaje algebraico
A continuación, te presentamos ejemplos
sobre la traducción o representación de lenguaje verbal a lenguaje algebraico.
Ten en cuenta que para llegar a esta representación empleamos variables o
incógnitas, las cuales se asignan con letra minúsculas del abecedario.
Por ejemplo, traducimos
o representamos en lenguaje algebraico los siguientes enunciados:
|
Lenguaje verbal |
Variables o incógnitas |
Lenguaje algebraico |
|
El
Taller 1 tiene el doble de paños matrimoniales de lo que tiene el Taller 2 |
Lo
que tiene T1: x Lo
que tiene T2: y |
2x = y |
|
Por
6 paños y 3 fajas se paga S/.1 560 |
Precio
del paño: z Precio
de la faja: t |
6z + 3t = 1 560 |
|
La
mitad de la producción de sombreros, menos la tercera parte de la producción de
alforjas equivale a 300 unidades |
Producción
de sombreros: p Producción
de alforjas: q |
|
2.2.- SISTEMAS DE ECUACIONES: Un sistema de dos
ecuaciones de primer grado con dos incógnitas tiene la forma:
Donde: a1, b1,
a2 y b2, son los coeficientes; x e y son las incógnitas; C1 y C2 Son los
términos independientes. El conjunto solución es el par de valores (x, y) que satisface simultáneamente
las dos ecuaciones.
2.3.- MÉTODOS DE RESOLUCIÓN DE SISTEMA DE ECUACIONES:
Existen 4 métodos básicos, para resolver
sistemas de ecuaciones lineales con dos incógnitas: Método de sustitución,
Método de igualación, Método de reducción y Método gráfico.
|
Método de reducción |
Método gráfico |
Método de igualación |
Método de sustitución |
|
1. Se elige la incógnita (la que te parezca más fácil de reducir).
2. Se hace que los
coeficientes de dicha incógnita, en las dos ecuaciones sean opuestos. 3. Se suman las dos
ecuaciones quedando, una ecuación con una incógnita que se resuelve. 4. Se sustituye en
cualquiera de las dos ecuaciones. |
1. Se despeja la incógnita y
en ambas ecuaciones. 2. Se construye, para cada
una de las dos funciones de primer grado obtenidas, la tabla de valores
correspondientes. 3. Se representan
gráficamente ambas rectas en los ejes coordenados. 4. En este último paso hay
tres posibilidades: a) Si ambas rectas se cortan, las coordenadas del punto de corte son
los únicos valores de las incógnitas x
e y. Sistema compatible
determinado. b) Si ambas rectas
son coincidentes, el sistema tiene infinitas soluciones que son las
respectivas coordenadas de todos los puntos de esa recta en la que coinciden
ambas. Sistema compatible indeterminado. c) Si ambas rectas son paralelas, el sistema no tiene solución.
Sistema incompatible. |
1. Se despeja la misma
incógnita de las dos ecuaciones (la que te parezca más fácil de despejar). 2. Se igualan las
expresiones quedando una ecuación con una incógnita. 3. Se resuelve la ecuación. 4. El valor obtenido para la
incógnita se sustituye en una de las ecuaciones y se opera para determinar la
otra. También se puede sustituir en una de las dos ecuaciones obtenidas en el
punto 1. |
1. Se despeja una incógnita
de una ecuación (la que te parezca más
fácil despejar). 2. Se sustituye en la otra
ecuación, quedando una ecuación de primer grado. 3. Se resuelve la ecuación. 4. El valor obtenido para la
incógnita se sustituye en una de las ecuaciones y se opera para determinar la
otra. |
2.4.1.- APLICACIÓN 1 (método de
reducción).
“Una vendedora lleva al mercado 80 kg de frutas, entre plátanos y
manzanas, cuyo importe total es de S/.536. El precio de cada uno de ellos es de
9 y 5 soles respectivamente ¿Qué cantidad de cada fruta
había?”
SOLUCIÓN:
i) Sean
las incógnitas: x = kg de plátanos
; y = kg de manzanas
ii) De los
datos representamos: La cantidad de kg entre plátanos y manzanas es 80,
entonces:
x + y = 80
El importe total es de 536
soles, sabiendo que el precio es de 9 y 5 soles respectivamente, entonces:
9x + 5y = 536
ii) El
sistema de ecuaciones quedaría:
iv)
Aplicamos el método de reducción, eliminamos “y” para ello multiplicamos por
(-5) la ecuación (i):
v )
Resolviendo para encontrar la variable "x":
4x = 136
x = 136/ 4
X = 34 plátanos
vi) Reemplazamos
el valor de “x” en la ecuación (i) para obtener el valor de "y":
X + y = 80
34 + y = 80
Y = 80 - 34
y = 46 manzanas
RESPUESTA: finalmente
podemos decir que: había 34 kg de
plátanos y 46 kg de manzanas.
2.4.2.- APLICACIÓN 2 (método gráfico).
“En una granja donde hay palomas y conejos, Sebastián cuenta 10
cabezas y 28 patas. ¿Halla el número de palomas y conejos?”
SOLUCIÓN:
Sean "x" palomas e "y"
conejos, además las palomas tienen 2 patas y los conejos 4 patas.
a) De los enunciados tenemos:
Sebastián cuenta 10 cabezas: x + y= 10
Sebastián cuenta 28 patas: 2x + 4y = 28
b) Formamos el sistema de ecuaciones:
c) Despejamos "y" en la primera
ecuación, luego tabulamos:
x + y = 10
y = 10 - X
Si x =1 entonces y = 10 - x =
10 - 1 = 9
Si x = 2 entonces y = 10 - x =
10 – 2 = 8
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
… |
|
y |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
.. |
d) Despejamos "y" en la segunda,
luego tabulamos:
2x + 4y = 28
y = (28 - 2x) : 4
Si x =1 entonces y = (28 - 2x) : 4 = (28 – 2(1)) : 4 = 26 : 4 = 6,5
Si x = 2 entonces y = (28 - 2x) : 4 = (28 – 2(2)) : 4 = 24 : 4 = 6
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
… |
|
y |
6,5 |
6 |
5,5 |
5 |
4,5 |
4 |
3,5 |
.. |
e) Graficamos
ambas ecuaciones y observamos que se interceptan en un punto (6,4) porque decimos que el sistema es
compatible.
RESPUESTA: finalmente podemos
decir que: tenemos 6 palomas y 4 conejos.
2.4.3.- APLICACIÓN 3 (método de igualación)
“Olga desea ponerse en forma y llegar a su
peso recomendado. Por ello, va a pedir informes a dos gimnasios donde le
brindan la siguiente información:
Olga evalúa ambas
posibilidades y desea saber ¿cuantos meses debe asistir al gimnasio
para pagar el mismo monto en cualquiera de los dos?”
SOLUCIÓN:
i) Determinamos con variables el número de meses y el monto a pagar:
Sea "x" el
número de meses e "y" el
monto total que se paga.
ii) Luego se definen las ecuaciones.
Para el gimnasio A: y = 150 + 100x
Para el gimnasio B: y = 350 + 50x
iii) Resolvemos el sistema lineal con el método de igualación e Igualamos
ambas expresiones:
150 + 100x = 350 + 50x
100x - 50x = 350 -150
50x = 200
x = 200 : 50
x = 4
iv) Hallamos el valor de y reemplazando el valor de (x) en
Cualquiera de las dos ecuaciones:
y = 150 + 100x
y = 150 + 100(4)
y = 150 + 400
y = 550
RESPUESTA. Para pagar lo mismo en cualquiera de los dos gimnasios, debe
asistir 4 meses. En ese tiempo, el
pago sería de S/.550,00
2.4.4.- APLICACIÓN 4 (método de sustitución)
“Una familia que
vive en una comunidad de la provincia de Tarma se dedica a elaborar vasijas de
arcilla. Durante tres días estuvieron trabajando el padre con el hijo juntos y
se dieron cuenta que en total hicieron 21 vasijas y que la diferencia entre el
número de vasijas que elaboró el padre con el número de vasijas que elaboró el
hijo es igual a 9 ¿Cuántas vasijas elaboró cada uno de
ellos?”
SOLUCIÓN:
Sean las variables: x = cantidad de vasijas que hizo el padre e y =
cantidad de vasijas que hizo el hijo
i) Los datos que nos proporciona son los
siguientes:
La suma de las vasijas que
hizo el padre con las vasijas que hizo el hijo es 21.
Luego la primera ecuación: x + y =
21
La diferencia ente la cantidad
de vasijas que hizo el padre con la cantidad de vasijas que hizo el hijo es 9.
Luego la segunda ecuación: x - y = 9
ii) Ahora, escribamos las dos ecuaciones,
que es un sistema:
iii) Despejamos “x” de la ii) y lo reemplazamos en la i):
x – y = 9 ….. ii)
x = 9 + y ….. iv)
Luego, reemplazamos en
la i):
x + y = 21
9 + y + y = 21
2y = 21 - 9
Y = 12 : 2
y = 6
Luego, reemplazamos
valor de “y” en la iv):
x = 9 + y ….. iv)
x = 9 + 6
x = 15
RESPUESTA: finalmente podemos
decir que: El hijo hizo 6 vasijas y el padre 15 vasijas.
TERCERA PARTE:
3.1.- VIDEOS DE REFURZO: Ingresar a los siguientes links y analizar:
1º.- LENGUAJE VERBAL
A LENGUAJE ALGERBARICA
https://www.youtube.com/watch?v=DV3C_RawfBg
2º.- METODOS DE
SOLUCION SISTEMA DE ECUACIONES.
https://www.youtube.com/watch?v=P_NBQQzM1UU
CUARTA PARTE:
4.1.-
Traducimos de lenguaje verbal a lenguaje algebraico. Completan una
tabla.
|
Lenguaje verbal |
Variable o incógnita |
Lenguaje algebraico |
|
Un numero Cualquiera. |
|
|
|
La Suma de dos números. |
|
|
|
Lu Diferencia de dos números. |
|
|
|
El producto de dos números. |
|
|
|
El cociente de dos números. |
|
|
|
El doble de un número. |
|
|
|
El triple del cuádralo de un número. |
|
|
|
La mitad de la diferencia de dos números. |
|
|
|
Cuatro veces la suma de dos números cualesquiera. |
|
|
4.2.-
Utilizando alguno de los
métodos tratados, desarrolla las siguientes situaciones:
1) Una familia, deseando
contar con todos sus familiares que viven en los caseríos de Monsefú para que estén
presentes en el matrimonio de su única hija; por lo que, ha contratado una flota de 22 camiones, unos de 4
ruedas y otros de 6 ruedas. Si en total se cuentan 108 ruedas ¿Cuántos camiones de 4 ruedas se ha
cont4ratado?
2) Para la celebración
de un matrimonio tradicional del distrito de Monsefú, se desea envasar 100
litros de vino en botellas de 2 y 5 litros. Si el total de botellas es 26 ¿Cuántos son de 5 litros?
3) Javier como
regalos de matrimonio, ha recibido 7 vehículos menores: bicicletas (2 ruedas) y triciclos (3 ruedas) ¿Cuántas bicicletas y cuántos triciclos ha recibido Javier, si
suman un total de 17 ruedas?
4) Comentando con mi padre,
dice: “Cada vez que voy a un matrimonio gasto
S/.15 en regalos y cada vez que voy a u bautizo gasto S/.25. Si he salido 20
veces (a un matrimonio o bautizo) y gasté S/. 360” ¿Cuántas veces ha ido a un bautizo?
5) Una familia, se está preparando para la celebración del matrimonio
del hijo mayor; por lo que, la madre comenta: “En mi corral, tengo cabritos y gallinas;
pero, he contado 68 cabezas y 222 patas”. Se pregunta preocupada: ¿Cuántas cabritos más que gallinas tendré?
QUINTA PARTE: Actividades de reflexión.
Después de haber realizado tu trabajo, reflexiona acerca de cómo resolviste todas las situaciones
problemáticas y qué estrategia usastes en las diferentes situaciones,
respondiendo a las siguientes preguntas:
¿Qué aprendiste?
¿Como lo aprendiste?
¿Para qué lo aprendiste?
¿Qué dificultades encontraste y que hiciste para superarlas?
¿Te será útil lo aprendido?
SEXTA PARTE:
6.1.- RETO: Después de recibir
una hoja impresa, por parte del docente, utilizando alguno de los métodos tratados, encuentra la totalidad de
colores rojos y amarillos usados, según la SITUACIÓN SIGNIFICATIVA planteada.
6.2.- ENTREGA: En
físico, de manera presencial.
¡
BUENA SUERTE ¡
Vallejos MARRUFO, Elías.
PROFESOR
“No digas ¡cuando tenga tiempo
estudiaré!, porque quizás nunca tendrás tiempo” (Hilel, Pirkei Avot)




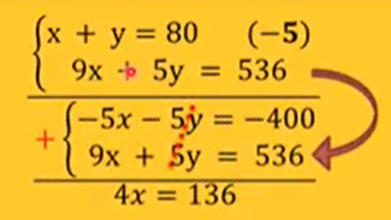







No hay comentarios:
Publicar un comentario